Proponen un nuevo conjunto fractal que en tres dimensiones tiene una características similares al conjunto de Mandelbrot (que se define en 2 dimensiones) y al que llaman conjunto mandelbulb.
|
|
|
Hay otros espacios a explorar que no son el espacio exterior. Son espacios abstractos habitados por objetos matemáticos. A veces su representación gráfica es increíblemente bella. Uno de los más famosos es el conjunto de Mabdelbrot que pertenece al plano complejo. Benoît Mandelbrot lo estudio en 1980 y por eso lleva su nombre, aunque en realidad éste fue descubierto por Pierre Fatou y Gaston Julia a principios del pasado siglo y representado por primera vez en 1978 Robert Brooks y Peter Matelski.
El conjunto de Mandelbrot, al estar contenido en el plano complejo, es plano. Sin embargo, posee una rica geometría. Es el arquetipo de fractal, de las figuras que son autosemejantes. Es decir, que cada parte, por pequeña que sea, tiene una forma similar a la de cualquier otra parte a cualquier escala.
Hay muchos ejemplos de fractales que se pueden construir de una manera sencilla. Uno de ellos puede ser el de la curva de Koch, que contiene un área finita bajo un perímetro infinito de dimensión fractal 1,26. Y es que otra característica de estos objetos es que tienen, en general, dimensión fraccionaria.
Además de estas características extrañas, el conjunto de Mandelbrot posee valor en Ciencias de la Computación. Se obtiene por recursión, iterando una función compleja (que usa números complejos) una y otra otra vez, concretamente esta fórmula:
zt+1 = zt2 + c
El algoritmo utilizado para representar el conjunto es como sigue:
Para cada punto c perteneciente al plano complejo.
– Fijar z0 =0
– Iterar desde t=1 hasta tmax
Calcular zt = z2t + c
Si |zt| > 2 salir del bucle
– Si t < tmax pintar c de blanco (el punto no pertenece al conjunto)
– Si t = tmax pintar c de negro (el punto pertenece al conjunto)
Como se puede apreciar, un punto pertenecerá o no al conjunto si el módulo del punto iterado tmax veces cumple o no una condición dada, si converge o no.
El conjunto, una vez llegamos a una profundidad de exploración dada por tmax, viene a ser algo así:

|
Los puntos coloreados (que no son negro) corresponden a números que no pertenecen al conjunto y para los que se ha asignado un color en función de lo supuestamente «lejos» que se han quedado de él. Si aumentamos mucho el número de iteraciones, y escogemos regiones cada vez más pequeñas, podemos apreciar la autosimilitud y la intrincada estructura de este objeto que algunos han llegado a calificar como monstruo. Es decir, aparecen nuevos detalles al aumentar la resolución, a todas las escalas estudiadas, e incluso aparecen “copias” del conjunto entero a resoluciones finísimas.
Lo más fascinante quizás sea que se puede demostrar que el conjunto de Mandelbrot es incomputable. Hay varios tipos de incomputabilidad, pero en este caso nos referimos a si podemos contestar la pregunta de si un programa se detendrá o no (un problema de decisión). Asumimos además que el programa que se quiere comprobar termina cuando alcanza una solución a un problema determinado y no lo hace si no la encuentra.

|
Alan Turing demostró que hay muchos problemas que no son computables y que, por tanto, algunas veces no podemos decir si un programa se detendrá o no. Una vez que un modelo de computación tiene la habilidad de estudiarse a sí mismo paga el precio de no ser capaz de parar bajo un conjunto apropiado de circunstancias (ciertas o erróneas).
Recordemos que Gödel demostró que todo formalismo matemático lo suficientemente complejo para que sea consistente es necesariamente incompleto. Pues bien, el teorema de Gödel es un caso particular del de Turing, ya que cualquier afirmación matemática puede ser implementada en un programa.
Por tanto la pregunta «¿Hay una demostración matemática para esta afirmación?» es equivalente a «¿Parará el programa?».
En realidad el algoritmo antes expuesto no representa el conjunto de Mandelbrot, sino una aproximación a él. Esto se debe a que hemos truncado el cálculo a una profundidad dada (tmax). Habrá puntos que hemos calificado como no pertenecientes al conjunto que si hubiéramos esperado más tiempo (más iteraciones) hubieran convergido y cumplido el criterio. Y da lo mismo si aumentamos el número de iteraciones, porque seguirá habiendo puntos para los cuales exista el mismo problema (y no sabremos a priori cuáles son). Esto quiere decir que para algunos puntos del plano complejo nunca sabremos si pertenecen o no a este conjunto tan singular.
Así que, como vemos, el conjunto de Mandelbrot da para mucho más que unas figuras atractivas. Pero como hay que captar la atención del lector de alguna manera podemos seguir con esta historia y publicar figuras realmente bonitas sobre este tema, concretamente sobre un nuevo conjunto, ente que además nos ha servido para contar todo lo anterior.
En los años ochenta hubo una auténtica fiebre por parte de los aficionados a la hora de calcular y representar el conjunto de Mandelbrot con mayor resolución, sobre todo a través del seguimiento que hizo Sicentific American (el que escribe todavía recuerda leer esos artículos sin entender mucho los detalles). Se inventaron atajos y algoritmos que permitían un cálculo que se hacía cada vez menos llevadero para lo ordenadores conforme se aumentaba la resolución.
Como todas las cosas, pasó de moda, pero desde entonces se esperaba descubrir conjuntos similares que tuvieran toda esta rica gama de características, a poder ser incluso en dimensiones superiores.
Lo más que se llegó a descubrir fue un conjunto similar en cuatro dimensiones del cual se representaban cortes tridimensionales que parecían bastante pobres.
Obviamente había fractales tridimensionales que se podían construir de manera sencilla, pero, o bien eran totalmente estocásticos, o bien completamente regulares. Ninguno captaba la filosofía del conjunto de Mandelbrot. Y los algoritmos de iteración que se proponía en 3D no mostraban un comportamiento fractal real. Los trucos de hacer girar sobre sí mismo al conjunto de Mandelbrot tampoco proporcionaban resultados satisfactorios.
Ahora se propone un conjunto contenido en el espacio tridimensional que, si bien no se ha demostrado que sea tan rico matemáticamente como el de Mandelbrot, sí produce imágenes comparables. Denominan al nuevo conjunto como «conjunto mandelbulb», se supone que por similitud fonética con el de Mandelbrot y porque se parece a un bulbo (bulb).
Daniel White, un británico aficionado al tema, posee una página web en donde muestra algunos ejemplos del conjunto mandelbulb calculados en los últimos dos años.
Para crear el nuevo conjunto White se vale de coordenadas esféricas y de una función iterada con una filosofía similar a la empleada en el caso del conjunto de Mandelbrot.
Las primeras versiones del algoritmo producían objetos que carecían del detalle fractal fino que tiene el conjunto de Mandelbrot, pero gracias al foro sobre fractales y a la cooperación con otros aficionados se ha llegado a una formula o fórmulas que producen objetos increíblemente bellos, aunque no sean equivalentes a un Mandelbrot tridimensional.
Todavía queda por introducir rigor matemático en este tema y está por ver si al final se consigue algo análogo al conjunto Mandelbrot en tres dimensiones, pero de momento nos podemos deleitar con unas bellas y góticas imágenes.
GALERÍA
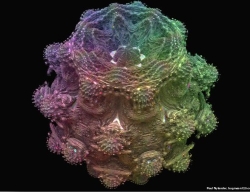
Esta figura representa el conjunto mandelbulb:
|
Aquí un detalle de ese conjunto calculado por David Makin:

|
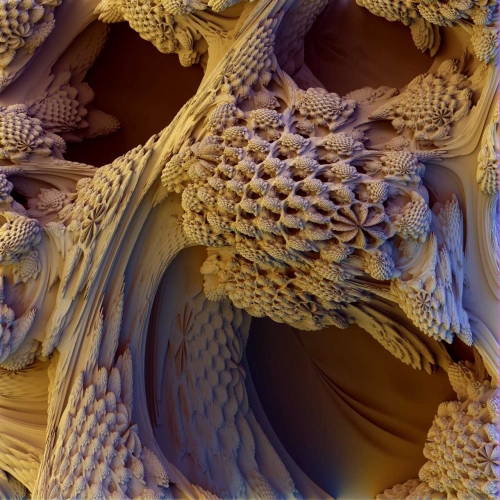
White llama a esta región del conjunto la cueva de los secretos perdidos:

|
A los aficionados a la coliflor romanesca les encantará esta imagen:

|
Ampliaciones sucesivas de la región anterior nos proporcionan:

|

|
Estas otras regiones evocan a corales submarinos:

|

|
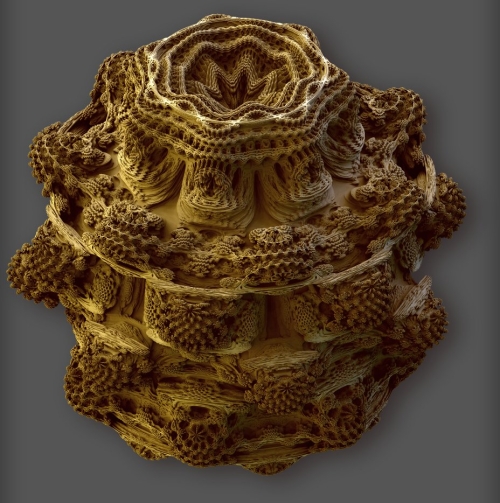
Según White esto recuerda a una colmena:
|
La espina de mandelbulb le será familiar a todo aficionado al conjunto de Mandelbrot:

|
Helado en Neptuno:

|
Para los amantes de los paisajes kársticos:

|
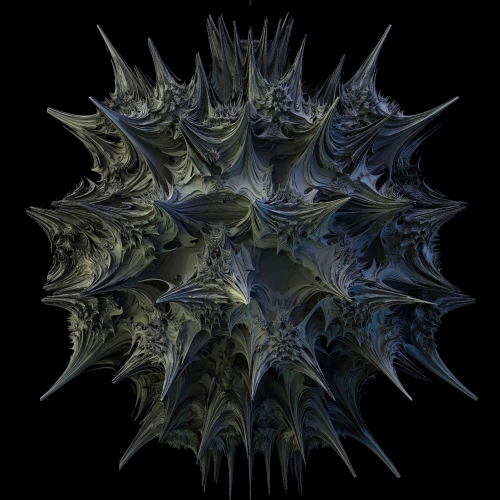
Las ecuaciones admiten variaciones que dan como resultado otros conjuntos igual de interesantes, como estos de aquí:
|

|
En la página web de White se pueden encontrar estas mismas imágenes en alta resolución y muchas otras, así como el algoritmo para obtenerlas.
Fuentes y referencias:
Página web de White. [1]
Vídeo 1. [2]
Vídeo 2. [3]
Vídeo 3. [4]
Vídeo 4. [5]
Página de Wikipedia. [6]
Ejemplo de imagen en alta resolución. [7]