NeoFronteras

Encuentran para el momento magnético del muón una diferencia con una significación estadística de 4,2 sigmas entre el valor teórico de consenso y lo medido por Muón g-2.

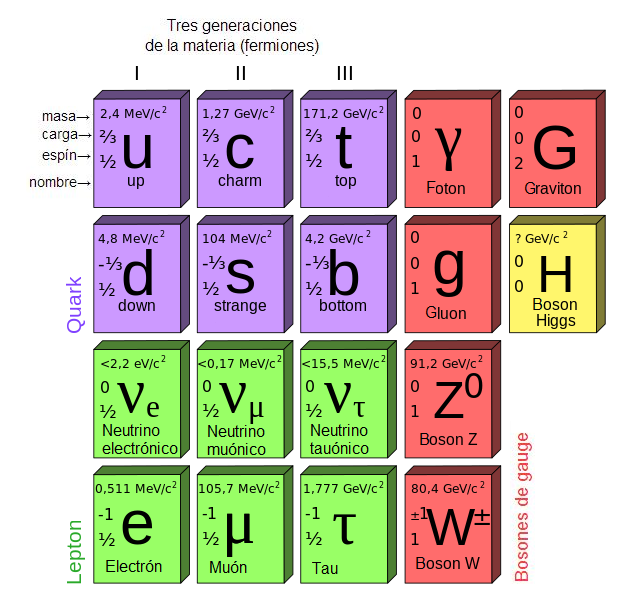
En el modelo estándar de partículas hay tres familias de partículas. Cada una de ellas con una pareja de quarks y dos leptones asociados de los cuales uno es un neutrino y el otro una partícula con carga eléctrica.

En la primera familia tenemos al electrón y al neutrino electrónico. En la segunda al muón y al neutrino muónico. En la tercera al tau y su neutrino asociado. El electrón, el muón y el tau son prácticamente la misma partícula, sólo cambian sus masas. El electrón es más ligero que el muón y este más ligero que el tau.

Así que el muón no es más que un electrón pesado, pero que no es estable, pues al cabo de un tiempo se desintegra. La única manera de hacer mediciones sobre ellos es que sufran la dilatación temporal relativista si se mueven a una buena fracción de la velocidad de la luz.

Todos los días miles de muones atraviesan nuestros cuerpos, son el subproducto de la interacciones de los rayos cósmicos con la atmósfera terrestre. Si llegan a la superficie es precisamente por esta dilatación relativista. Pero si los queremos estudiar con detenimiento es mejor colocarlos en un acelerador de partículas, preferiblemente circular, como en el experimentos Muón g-2 (ver foto de cabecera). Gracias a que viajan a una velocidad relativista dentro de este anillo, los muones parecen tener una vida media de 30 microsegundos. Algunos vivirán menos, pero unos pocos pueden vivir muchos más, lo suficiente como para poder medir muy bien su momento magnético.

Una de las propiedades que podemos medir del muón es este momento magnético o g, que es una propiedad que hace que actúe como un pequeño imán. El experimento Muón g-2 mide desde hace un tiempo ese momento magnético con increíble precisión.

El experimento Muón g-2, ahora situado en el Fermi National Accelerator Laboratory o Fermilab (Batavia, Illinois), empezó a funcionar por primera vez entre 1997 y 2001 en el Brookhaven National Laboratory (Long Island, Nueva York). Los resultados originales, anunciados en 2001, encontraron que el momento magnético del muón era distinto a lo esperado por el modelo estándar. La medida del campo magnético era ligeramente mayor de lo que predijo la teoría. Esto causó cierta sensación y provocó controversia entre los físicos. Algunos físicos teóricos esperan que el Modelo Estándar no sea la última palabra y que haya una nueva física más allá de él. Es decir, que haya nuevas partículas elementales por descubrir. De otro modo se quedarían sin objeto de estudio.

Recordemos que, pese a lo poderoso que es el colisionador LHC, no se ha descubierto ninguna partícula nueva además del bosón de Higgs. Sólo se han hallado combinaciones de partículas, estados excitados de las ya conocidas o resonancias.

Los resultados anteriores de Muón g-2 sostenían esta discrepancia con una significación estadística no muy alta, pero en el pasado día 7 se han hecho públicos los nuevos resultados, que tienen una significación estadística más alta, en concreto con 4,2 sigmas. La política actual es que se declare un descubrimiento en Física de Altas Energías sólo si se tiene una significación de 5 sigmas o mayor.

El experimento Muón g-2 consiste en un acelerador de partículas de 15 metros de diámetro por el que circulan muones. Un poderoso campo magnético de unos 1,5 Tesla generado por un imán de 680 toneladas mantiene a los muones en su trayectoria circular y, al mismo tiempo, hace girar su eje magnético. Cuanto más fuerte sea el momento magnético de las partículas, más rápido girará el eje, como en una peonza. Lo que se mide es la velocidad a la que el giro del muón precesa en el campo magnético.

En una primera aproximación, la Física predice que las partículas elementales como el muón y el electrón tienen un momento magnético que es exactamente igual a 2 dos veces el momento magnético de Bohr. Sin embargo, si usamos la Teoría Cuántica de Campos se puede calcular una desviación de ese valor.

El espacio está lleno de una serie de campos cuánticos que lo permean completamente. El vació no es un ente sin nada, sino que tiene propiedades. Estos campos pueden excitarse y a esas excitaciones las llamamos partículas. Cuando una partícula se desintegra en otras, su energía va de un campo a otro en sucesivas excitaciones. Además, estos campos pueden fluctuar, y estas fluctuaciones pueden ser interpretadas como «partículas virtuales» que «aparecen» en pares partícula-antipartícula.

Así que el espacio alrededor de cualquier partícula hierve de estas partículas virtuales, por lo que el espacio vacío nunca está realmente vacío y altera las propiedades de las «partículas reales». Así que un muón solitario (u otra partícula) nunca puede ser observado en solitario, sino apantallado y alterado por «partículas virtuales». De hecho, lo que es realmente una partícula en concreto es siempre ella y sus circunstancias. Si pudiéramos medir partículas aisladas del vacío (algo imposible) tendrían distinta masa, carga o momento magnético de los conocidos.

Bajo los diagramas de Feynman se puede calcular las distintas contribuciones que los campos del vacío tienen sobre una partícula en concreto. Como, por ejemplo, las contribuciones al momento magnético del electrón o del muón debidas al resto de los campos cuánticos de las otras partículas conocidas. No solamente por su mera existencia, sino por los distintos tipos de interacción con estas partículas virtuales. Además, las partículas más ligeras, y que, por tanto, pueden fluctuar del vacío más fácilmente, tendrán contribuciones más importantes. Por el contrario, las partículas más pesadas tendrán menos contribuciones porque es más difícil hacer fluctuar su campo.

En el lenguaje de las partículas virtuales y de la carga del electrón es fácil visualizar el fenómeno. Un electrón tendría una carga eléctrica «desnuda» dada, pero a su alrededor aparecerían pares virtuales de electrón-positrón. Estos dipolos se colocarían con los positrones apuntando hacia el electrón real por tener carga contraría y apantallarían su carga «desnuda». Así, desde lejos, vemos una carga que es distinta a la «desnuda». De hecho, no es posible observar la carga «desnuda» y siempre observamos la carga «vestida». Ni siquiera sabemos el valor de la carga «desnuda» del electrón o del muón. Sólo sabemos la carga «medible».

Como el electrón o el muón tienen spin (de valor 1/2), también habrá un acoplamiento magnético con el vacío y sus momentos magnéticos medidos serán diferentes a sus valores para sus momentos magnéticos «desnudos». En este caso sí se puede calcular teóricamente el momento magnético «desnudo» del electrón o del muón, que es 2 veces el momento magnético de Bohr.

Ahora, podemos tener en cuenta casi todas las partículas conocidas que aparecen en el Modelo Estándar y calcular sus contribuciones de vacío, bajo las interacciones conocidas, al momento magnético del electrón o del muón y eso nos da un número. Si entonces medimos ese momento magnético con relativamente alta precisión no se verá ninguna diferencia respecto al valor teórico, que se puede calcular con unos 10 decimales. Se necesita una precisión mayor.

El problema es que si elegimos el electrón como partícula de prueba hay que calcular bien las contribuciones, pues sus interacciones complican mucho el cálculo teórico, sobre todo lo relativo a los bosones de la interacción electrodébil, pero también debido a la interacción fuerte (cromodinámica cuántica). Sin embargo, si nos quedamos con los muones, estas contribuciones pueden ser más pequeñas al depender de las masas, pues el muón es unas 200 veces más pesado que el electrón. Digamos que es más fácil calcular el momento magnético para el caso del muón que para el electrón.

Ahora supongamos que hay más partículas que no conocemos, es decir, supongamos que hay más campos cuánticos rellenando el vacío que los predichos por el Modelo Estándar. Al ser partículas muy pesadas (de otro modo las podríamos haber «materializado» ya en el LHC y similares), esos campos son difíciles de excitar, por lo que se generaran pocas partículas virtuales de esos campos y su contribución al momento magnético del muón será muy pequeña. Es decir, aparecerán como cambios en los valores decimales más lejanos por la derecha de la coma decimal. Así que para poder medir esas «anomalías» hay que medir el momento magnético del muón con muchísima precisión. Esto es precisamente lo que hace el experimento Muón g-2.

El valor que se ha publicado el otro día es g = 2.00233184122(82), que se puede comparar con la predicción teórica de consenso de junio 2020 que usa el Modelo Estándar, que es g_MS = 2.00233183620(86). También podemos obviar el valor de base 2 para expresar solamente la anomalía a = (g−2)/2, que para el valor medido nos da un valor de a = 0.00116592061(41) y compararlo con el valor teórico a_MS = 0.00116591810(43). Las cifras entre paréntesis corresponden a la barra de error en los dos últimos decimales mostrados.

Como se puede observar, hay una diferencia entre las dos, lo que indicaría que hay otras partículas distintas a las conocidas. Pero lo más importante a insistir es la significación estadística, que, de momento, no llega a 5 sigmas. Todo el resultado podría ser al final el producto de fluctuaciones estadísticas y que la anomalía no existiera, pero esto no parece probable.

Estos resultados ahora publicados están basados en la primera de las cinco tomas de datos previstas, en concreto la de 2018. Ahora están trabajando con los datos de la segunda toma de datos de 2019 y también se tienen los datos de 2020. Todavía quedan dos tomas de datos de las previstas. Se espera que para 2025 se tenga con Muón g-2 un resultado con un mínimo de 7 sigmas de significación y una máximo de 12 sigmas.

Estaremos más seguros respecto al valor experimental cuando se dé una confirmación adicional e independiente. Eso podría provenir de otro experimento, aún en desarrollo, que usa una técnica distinta y que se está montando en el Complejo de Investigación del Acelerador de Protones de Japón (J-PARC) cerca de Tokai. Este experimento medirá el momento magnético del muón de una manera radicalmente diferente y se esperan sus primeros resultados para 2028.

Conforme se sigan acumulando más datos, se superarán las 5 sigmas y quizás se declare el descubrimiento de una física más allá del Modelo Estándar si hay un buen consenso respecto al valor teórico, pero este es precisamente el principal escollo.

Cabe dentro de lo posible que haya errores de cálculo en el resultado teórico de consenso predicho, que es un cálculo muy complicado y sucio, principalmente debido a la contribución cromodinámica. El foco está ahora precisamente en la estimación teórica para que incluya bien la contribución cromodinámica y se esperan muchos artículos al respecto. De hecho, algunos resultados teóricos al respecto realizados con cálculos cromodinámicos en el retículo en una supercomputadora ya apuntan a un valor teórico del momento magnético del muón prácticamente igual al medido por Muón g-2.

Así que, de momento, no se puede afirmar que el Modelo Estándar sea incorrecto.

Copyleft: atribuir con enlace a https://neofronteras.com

Fuentes y referencias:
Artículo original.
Preprint en ArXiv.
Artículo original.
Preprint en ArXiv.
Preprint en ArXiv.
Foto: Reidar Hahn/Fermilab.
Esquema Modelo Estándar: Wikipedia