Sobre la interpretación del principio de Heisenberg
Un experimento permite distinguir entre dos interpretaciones distintas del principio de incertidumbre de Heisenberg.
|
Una de los principios más misteriosos e interesantes de la Mecánica Cuántica es el principio de incertidumbre (o indeterminación) de Heisenberg. Nos dice que hay límites a lo que podemos conocer sobre los sistemas cuánticos.
Así por ejemplo, si nos fijamos en la versión que relaciona la cantidad de movimiento (o momento) de una partícula y su posición nos dice que cuanto mejor conozcamos la posición de una partícula peor conoceremos su cantidad de movimiento (el producto de su masa y velocidad o momento) y viceversa. Estas dos cantidades conjugadas (posición y momento) no son las únicas, así por ejemplo, el tiempo y la energía también tienen su propia relación de incertidumbre. Se pueden buscar otras cantidades conjugadas que sufran de lo mismo.
Se considera a Heisenberg el padre de la Mecánica Cuántica (MC). Cuando introdujo su famoso principio en 1927 imaginó en un experimento mental a un electrón que es observado con un microscopio basado en fotones de rayos gamma. De este modo cuando se quisiera medir la posición del mismo con un error ε(q) se podía alterar su momento en una cantidad η(p) que estarían regulados por la relación ε(q)η(p) ≥ h/4 π (siendo h la constante de Plank). Digamos que la medida altera el estado del sistema de tal modo que no podemos saber ciertas cantidades simultáneamente mejor de lo que nos dice esa relación. Esta relación tendría en cuanta el error en la medición.
Ese mismo año, Earle Kennard, propuso otra relación de incertidumbre muy similar en la forma, pero conceptualmente distinta. En esta formulación el principio de incertidumbre dice que σ(q)σ(p) ≥ h/4π. En este caso viene a decir que las fluctuaciones cuánticas de la posición y del momento no se pueden suprimir simultáneamente por debajo de cierto límite. Si reducimos las fluctuaciones en uno las aumentamos en el otro. Esto expresaría un concepto más estadístico y universal en el que se tendría en cuanta la dispersión (a través de la desviación típica).
Aunque desde entonces algunos han creído que ambas formulaciones son básicamente la misma y que ambas describen el mismo fenómeno, en realidad no es así. Como se puede observar, la ecuación es prácticamente la misma, pero conceptualmente son muy distintas. En el primer caso parece tratarse de una torpeza nuestra a la hora de medir y en la segunda a algo intrínseco al sistema. Los físicos usan la formulación de Kennard en la actualidad.
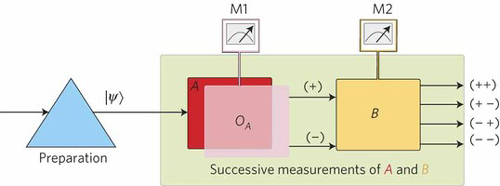
Este tipo de situaciones en las que hay varias interpretaciones son habituales en MC y no suelen solucionarse debido a que es muy difícil diseñar un experimento que las distinga. Pues bien, unos físicos de las universidades de Viena y Tokio dirigidos por Yuji Hasegawa han realizado un experimento con neutrones que permite distinguir entre estos dos casos. En lugar de medir la relación posición-momento han medido dos componentes ortogonales del estado de polarización del spin de los neutrones de un haz (algo equivalente bajo del principio de incertidumbre que mide otras dos cantidades conjugadas). La conclusión es que la interpretación de Heisenberg es incorrecta y que la correcta es la de Kennard, que es la que se viene usando en la Física moderna desde hace mucho tiempo.
En el experimento se preparó un haz de neutrones en el que se midió dos componentes spin simultáneamente en clara violación del principio de incertidumbre según la interpretación original. La otra interpretación se mantuvo. El resultado, de haber sido el contrario, hubiera sacudido los cimientos de la Mecánica Cuántica moderna.
Este resultado se ha conseguido gracias a que en 2003 Masanao Ozawa (Universidad de Nagoya) llegó a una expresión del principio que permitía describir tanto el error como las fluctuaciones: ε(q) η(p) + σ(q)η(p) + σ(p)ε(q) ≥ h/4π.
En el experimento se pudo precisamente distinguir entre errores en la medida y fluctuaciones. Algo sorprendente cuando muchos físicos habían pensado que la única manera de reducir los errores es suprimiendo las fluctuaciones. Pero la desigualdad de Ozawa sugiere que hay otra manera de reducir errores al permitir al sistema tener grandes fluctuaciones, aunque suene contradictorio.
Pero en el mundo real el error en la medida siempre está ahí, sumándose a las fluctuaciones, así que desde el punto de vista experimental y práctico la formulación de Ozawa resulta útil al tener en cuenta tanto fluctuaciones como errores en la medida y su alteración provocada por el acto de medida.
Cuando se divulga la MC se suele expresar la idea ingenua de que la relación de incertidumbre surge porque la medida experimental de una cantidad X da al traste con la medida de la cantidad complementaria Y. Este experimento ayudar a eliminar esa idea.
No es que seamos torpes a la hora de medir cantidades conjugadas, es que por muy bien que lo hagamos es imposible medirlas con precisión debido a sus fluctuaciones inherentes. Sí, la MC es tan rara como siempre se ha creído, incluso más de lo que cree la gente común.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=3765
Fuentes y referencias:
Noticia en Physicsworld.
Noticia en Scientific American.
Artículo original.
40 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





lunes 12 marzo, 2012 @ 8:52 am
Como dice el artículo, no podemos asirnos, los muy flojos en MC a la interpretación de Heisenberg. Porque siempre podríamos soñar en que, si M y P son magnitudes conjugadas y, al medir una de ellas, se altera la otra, conociendo finamente la energía enviada y su acción sobre P, p. ej., podríamos, de algún modo, calcular el cambio producido en M. Pues no señor. Sin duda esto cuadra mejor con la íntima realidad estadística de la materia que habremos de aceptar sin paliativos.
Saludos desesperados pero con mucha voluntad de aceptar lo demostrado.
lunes 12 marzo, 2012 @ 9:58 am
Si no lo he entendido mal, para que Ozawa esté en lo cierto se tiene que cumplir que seamos capaces de mensurar las fluctuaciones con gran precisión, cosa que ignoro debido a mis limitaciones en esta materia:
¿es posible mensurar esas fluctuaciones con alta precisión?
Saludos y abrazos
lunes 12 marzo, 2012 @ 1:24 pm
Excelente artículo y excelente explicado. Neofronteras me asombra con la calidad de las explicaciones y detalles. Cuando salen noticias como estas en otras webs, poco se entiende y siempre espero a que aquí lo expliquen como corresponde. Se me aclaró perfecto el punto de vista de heinsenberg algo ambiguo y desconcertante, con el nuevo punto de vista coherente y con causa.
lunes 12 marzo, 2012 @ 6:20 pm
Clarificador este artículo.No conocia la inecuación de Ozawa, ahora ya sí.En cuanto a las cantidades conjugadas «tiempo-energía», hay una forma sencilla de materializar físicamente el principio de Incertidumbre, que relaciona la frencuencia (energía) con el intervalo de tiempo que es caracteristico del ritmo de cambio del sistema, sólo hay que encender el interruptor de la luz y si hay una radio cercana, se puede oir un ruido estático.Esto sucede porque la cantidad de electricidad que transportaba el cable cambia muy rapidamente al darle al interruptor con lo que el rango de frecuencias debe ser grande y ello es recogido por el aparato de radio como ruido estático.
miércoles 14 marzo, 2012 @ 10:26 pm
Lo que no me queda del todo claro es cómo podemos saber si la realidad es o no indeterminada; es decir, ¿cómo podemos saber que nuestro conocimiento de la realidad física -fluctuaciones a nivel cuántico, en este caso- no esta determinado por nuestros modelos explicativos? Mi propio profesor de teoría del conocimiento, quien adopta en la asignatura un enfoque multidisciplinar y complejo, no fue capaz de responderme a la pregunta acerca de si el principio de incertidumbre de Heisenberg es intrínseco al sistema o, si por el contrario, es un simple defecto de nuestra capacidad de conocer. ¿Es la ciencia, en este sentido, prejuiciosamente realista? Espero respuestas para este inquieto admirador de la ciencia.
jueves 15 marzo, 2012 @ 12:50 am
Buena pregunta.
Es que no es fácil saber si un modelo físico responde a una realidad ontológica o si es pura epistemología. ¿Hay diferencia entre si algo no se puede conocer o si nosotros nunca lo podremos conocer?
La realidad física suele estar siempre un poco más allá de nuestros modelos, es inasible, se escapa.
Entre los físicos teóricos no hay consenso sobre muchas cosas, ¿es el tiempo un ente real o es un fenómeno emergente de una subestructura? A falta de buenas teorías a veces sólo hay opiniones.
Pero incluso con buenas teorías a veces tampoco hay consenso. Entre los físicos cuánticos se tiende a creer que la incertidumbre es inherente al sistema, a la realidad misma (es ontológica) y no debida a nuestra incompetencia. Pero siempre se puede creer en variables ocultas y que de algún modo toda esa incertidumbre desaparezca.
Realismo, no localidad, etc. son términos que dan para muchas discusiones en este campo y que muchas veces no están bien definidos.
Lo que parece claro en este campo y en otros es que hay límites absolutos intrínsecos al conocimiento. Hay cosas que que no podremos saber jamás, por muy inteligentes que seamos. Los trabajos de Turing, Gödel y demás así lo parecen indicar. Ni siquiera son posibles todas las matemáticas concebibles.
Quizás haya una teoría que esté más allá de la cuántica, pero puede que sea aún más rara.
El Universo, aunque sea infinito e ilimitado, parece estar constreñido por ciertos límites dados por leyes naturales: la velocidad de la luz, la incertidumbre cuántica, etc. Va contra nuestros deseos, pero el Universo es siempre ciego y sordo a nuestros deseos o anhelos e indiferente a nuestras frustraciones. Pero nosotros somos el Universo estudiándose a sí mismo. El Universo está es nosotros, formamos parte de él. Quizás de ahí vengan los problemas.
La pregunta es si estas leyes son las únicas posibles, si existe una Parafísica que cree físicas distintas en distintos universos y si hay libertad para crear cualquier cosa. Quizás no haya tal libertad. Einstein se preguntaba si Dios (un Dios raro del tipo Spinoza en el que él «creía») tuvo libertad para crear las leyes físicas.
Por lo que se sabe la nada es inestable y tiende a fluctuar y producir espacio, materia, universos… Sería curioso que la inestabilidad de la nada no pudiera dar lugar a cualquier cosa.
Al final los físicos se conforman con disfrutar por el camino y dejan las preguntas últimas para los filósofos, se preguntan más por el cómo que por el por qué. Quizás esas preguntas últimas nunca tengan respuesta o sean preguntas ilegítimas.
Feynman comparaba la labor de los físicos con la tarea de pelar las infinitas capas de una cebolla, siempre hay una nueva debajo, pero para él lo importante era el placer de «finding things out».
jueves 15 marzo, 2012 @ 8:30 am
Estoy alucinado. Es temprano. Acabo de desayunar y al releer la sencillez del 4 de lluís, la envidiable profundidad de la pregunta de Daniel y la magistral respuesta de Neo, me parece estar contemplando una extraordinaria obra de arte, de esas que elevan el espíritu sobre la humana condición.
Por cierto que este profundo Daniel no puede ser el mismo que aquel que nos enviaba a ver los toros, a hacer reverencias a nuestro rey y -creo recordar- despreciaba todo lo español, incluso el idioma que, sin embargo, él estaba empleando. Como no es posible que sea el mismo, pregunto: ¿No sería aconsejable alguna forma de evitar que idéntico nombre fuese utilizado por dos comentaristas distintos?
Es de agradecer -muchísimo, estimado Neo-, tu dedicación. ¿Cuando duermes?
Un sincero abrazo por haberme hecho disfrutar tanto de buena mañana, como por aquí se dice.
jueves 15 marzo, 2012 @ 8:51 am
Por cierto que a esa «nada fluctuante» habría que buscarle otro nombre porque me recuerda al +1-1=0, que sería esa nada por ser cero, pero que, en realidad es +1 y -1 que serán cero, pero no «nada». Para mí la nada carece de límites puesto que la llamamos así. Otra cosa sería el vacío, quizá sin materia y a lo mejor sin energía que lo atraviese, pero limitado por otros entes.
Bueno, yo me entiendo.
jueves 15 marzo, 2012 @ 9:43 am
Apreciado Tomás:
Gracias por sus palabras. Se hace lo que se puede. Alguien dijo que la pasión por la ciencia es como estar enamorado, uno quiere que todo el mundo lo sepa.
Este Daniel es distinto a aquel otro Daniel que menciona.
En cuanto a la nada o el vacío es una cuestión histórica, la nada se va redefiniendo según se van encontrando definiciones de vacío. Para un griego clásico un espacio convencional sin aire era la nada. Para nosotros hay vacíos de espacio-tiempo a partir de los cuales puede fluctuar un espacio-tiempo que cree un universo. Quizás en un futuro haya gentes que sepan que hay vacíos a partir de los cuales surgen físicas distintas. De nuevo es la cebolla de infinitas capas. Lo que no está claro es que el método científico nos siga funcionando por mucho tiempo en estos contextos.
jueves 15 marzo, 2012 @ 11:22 am
Es verdad, esto de compartir el conocimiento puede conducirte con facilidad a alcanzar una dicha duradera por dos razones fundamentalmente: porque es una actividad altruísta, de victoria-victoria y lo que es mas importante, porque nos puede hacer sentirnos implicados en algo que consideramos útilo, importante y beneficioso para otros seres.
Además las actividades que requieren esfuerzo como la Ciencia, nos provocan mayor satisfacción que actividades sencillas como comerse un dulce. Martin Seligman y Csikszentmihalyi apoyan esta idea de que la felicidad hay que ganársela, o sentir que nos la ganamos con cierto esfuerzo. Me viene a la cabeza el ejemplo del lagarto de Seligman, que no comía a pesar de disponer de todo tipo de manjares hasta que un dia a alguien se le cayó un bocadillo envuleto en papel de aluminio y el lagarto se acercó, rasgó con las uñas el papel y comió: su cerebro necesitaba un program similar al que se encontraría en estado salvaje, donde la comida no te viene a la boca.
Saludos y abrazos
viernes 16 marzo, 2012 @ 10:54 pm
Muy buenas. A partir de ahora pondré como nombre Daniel-20 para que no os confundáis. Me alegra ver la pasión que en este espacio hay por la ciencia y el conocimiento. La respuesta de Neo -aun no siendo definitiva, por supuesto- es de agradecer, pues le acerca a uno a esos límites, esos bordes que rozamos cuando hacemos ciencia. Me entusiasma ver que hay otras personas que intentan acercarse a todo estas cuestiones lo menos prejuiciosamente posible. Dicho esto, me gustaría saber cuál es vuestra opinión en relación a la mecánica cuántica. Dejemos de un lado la dicotomía onto-epistémica (realidad-modelo), ¿qué supone la mecánica cuántica para nuestra visión del mundo? No sé porqué, pero parece ser que todavía no somos conscientes de todas sus consecuencias. ¿Qué pensáis?
Un saludo y abrazo a todos.
sábado 17 marzo, 2012 @ 9:41 am
Estimado Daniel-20:
Aunque seguro que hay compañeros que te responderán con más conocimiento, aportaré mi cuota. La MC me produce vértigo e inseguridad. Me molesta, pero me consuela, p. ej., que la dualidad onda-partícula -a la que culpo de todo lo demás- pueda resumirse en energía y que ésta puede tomar muchas formas.
Como dices, es seguro que no somos conscientes de todas sus consecuencias, aunque ello es algo común y compartido con todas las formas del saber, máxime en aquellas ramas en las que ahora se está investigando y progresando tanto.
Has iniciado un tema interesante y espero que alguien te responda con más tino que yo.
Un cordial saludo.
sábado 17 marzo, 2012 @ 10:12 am
Quizá el problema con la mecánica cuántica (filosóficamente hablando) no sea su «rareza», que a fin de cuentas es un concepto relativo. Nos parece «rara» porque vivimos en un mundo «grande» donde los efectos cuánticos no son apreciables a simple vista y estamos acostumbrados a que los objetos no estén en dos sitios a la vez y no puedan comunicarse «fantasmalmente» a distancia (para una partícula esto sería lo realmente raro). Para mi la pregunta del millón es: ¿Por qué son tan diferentes los mundos microscópico y macroscópico?
Y no, no me convencen los ideas estadísticas de los «grandes números». Me parecen una petición de principio.
Saludos
sábado 17 marzo, 2012 @ 2:18 pm
Metiéndome de lleno:
La interpretación «clásica» de la Escuela de Copenhage encabezada por Bohr sostiene que el objeto del conocimiento es la experiencia antes que la realidad.
Sin embargo esta interpretación podría ser completamente errónea, del mismo modo que también lo puede ser la concepción empirista de la causalidad de Hume, que adolece de no considerar el papel del azar. Es decir, eliminamos el azar porque nos molesta para hacer nuestros cálculos y al final llegamos a conclusiones equivocadas.
La interpretación de Ozawa trata de dar la vuelta a este enfoque.
Según Mario Bunge,David Bohm y Einsstein se equivocan al pensar que le realsimo exige que toda variable dinámica tenga un valor preciso en todo momento y circunstancia. Según Bunge el «principio de inncertidumbre» sería incorrecto y la incertidumbre no sería mas que un «estado de ánimo».
Abrazos con azar.
sábado 17 marzo, 2012 @ 2:41 pm
Para Bunge, que nunca se apunta a las modas del momento, el Principio de incertidumbre no es un principo sino un teorema. Si es un teorema hay que ver si son válidas sus premisas, y de este análisis Bunge deduce que la fórmula no se refiere a una partícula concreta, sino que tiene un caracter general. Bunge la equipara a la «Ecuación de Schrödinger» y dice que ambas son «leyes de la naturaleza».
domingo 18 marzo, 2012 @ 1:12 am
Si de algo sirve la Mecánica Cuántica (MC) a algunos es para vivir del cuento. Cójase el principio de incertidumbre, sazónese con un poco de filosofía barata, añádase una pizca de religión oriental y hornéese con un poco de misticismo y ya se tiene un mal libro de Mecánica Mágica. Listo para llenar los bolsillo de listos sin escrúpulos. Hay que tener mucho cuidado con lo que se lee y a quien se lee.
Para cualquier físico medianamente instruido la MC es rara en tanto en cuanto tiene problemas de interpretación, pero con ella calcula muy bien. No es esoterismo. La mayoría de cantidades medibles que predice se obtienen mediante conceptos convencionales de Estadística. Así, se puede definir una desviación estándar que mida la dispersión en las medidas de un observable. La manera de ver la MC que se ve ahora es desde este punto de vista estadístico. Si se toman esas definiciones de dispersión se puede definir el producto de dos observables (representados como operadores autoadjuntos) como una expresión (un valor esperado) en la que aparece el conmutador de esos operadores . Si conmutan se obtiene cero y no hay relación de incertidumbre. Y si no conmutan da una cantidad distinta de cero y tenemos la relación de incertidumbre.
Decir que eso es un teorema no es correcto. Un teorema es una deducción lógica demostrable a partir de axiomas en las Matemáticas. Hay una libertad total a la hora de elegir esos axiomas y obtener distintos tipos de matemáticas.
Se puede reescribir la MC para que el principio de incertidumbre pueda parecer un teorema, pero eso no aporta absolutamente nada, ni a la MC ni a su interpretación.
En Física da igual que haya consistencia lógica y que sus postulados (los equivalentes a los axiomas) sean correctos o no. Si las conclusiones no se corresponden con lo que se mide se manda toda la teoría a la basura. No hay libertad.
La MC por otra parte es más cotidiana de lo que creemos, aunque no la usemos para fabricar automóviles. Es convencional desde hace 70 años. No es mágica. Si fuéramos habitantes de una estrella de neutrones hasta nos parecería de lo más natural.
Mario Bunge tiene el logro de haber calificado el psicoanálisis como pseudociencia. Pero no es un experto en cuántica. Se ha dedicado a muchos campos, incluyendo la Metafísica.
Opiniones las tenemos todos, pero no todas son relevantes. Tampoco son importantes. Lo único que necesitamos son experimentos que digan cosas y hasta ahora ninguno parece diseñado para distinguir interpretaciones.
El problema de base es que los seres humanos creemos no solamente que podemos saber y conocer todo, sino que todo es cognoscible. Quizás la MC nos está diciendo que hay aún más límites al conocimiento de lo que creímos o esperábamos, que por mucho que nos empeñemos no podemos saber ciertas cosas con precisión independientemente de nuestra habilidad. Si se acepta eso no hay demasiados problemas.
De nuevo la ciencia nos dice cómo son las cosas no por qué son así.
domingo 18 marzo, 2012 @ 10:00 am
Estimado Miguel Angel:
No puedo compartir la existencia del azar, pues si existiera, la causalidad, el método científico y la ciencia con él, no podrían existir. Soy absolutamente determinista pero estoy seguro de que no todo es determinable. Es más, diría que la mayor parte del Universo -macro y micro- nos es tan desconocido que sólo a una pequeña parte tenemos acceso. Como viene a decir Neo al final de su 16, no todo es cognoscible. Hay límites que nunca podremos superar. E incluso existirán entes y leyes de los que jamás tengamos noticia.
Mis mejores saludos.
domingo 18 marzo, 2012 @ 12:40 pm
Estimado Neo:
Su generoso 16 admite alguna matización por mi parte. Comienza dando una receta de» Mecánica Mágica» y «filosofía barata» para contestar a continuación de la cuestión de la incertidumbre y de si es o no un teorema, con lo cual cabe la duda de si en lo de la «filosofía barata» se refiere también a Bunge, aunque directamente no lo diga.
A continuación lo cita para decir que no es experto en MC y que ha escrito también sobre metafísica. Pero claro si aplicamos el mismo rasero podemos excluir a Max Planck por haber escrito mucho sobre metafísica también. Y a Tesla o Da Vinci por haber estudiado distintas disciplinas.
El concepto de teorema está claro en matemáticas, pero es espinoso cuando pasamos a la Física (tal vez no deberíamos hablar de teoremas en Física sino simplemente de axiomas).
Aún así, no se equivoca Bunge en cuanto al tema de la libertad pesto que considera que el teorema se deriva de axiomas básicos de la MC (por tanto no hay libertad como usted dice), por eso lo acaba comparando con lo que el llama «una ley de la naturaleza».
Bunge es trasngresor y ha acuñado algunos conceptos como el de «cuantón» tratando dar un nuevo enfoque a la dualidad: porque al final lo llamemos onda o partícula ¿con qué trabajamos en MC con ideas o con partículas físicas reales? Según Bunge la realidad existe y no es un enfoque correcto estudiar la MC (ni ninguna otra Ciencia) bajo el enfoque de que estamos estudiando ideas y no entes físicos
domingo 18 marzo, 2012 @ 12:58 pm
Estimado tomás:
Para negar por completo el azar necesitas recurrir a algo que no se ha descubierto todavía (variables ocultas).
De todos modos no hay mucho donde discutir cuando te he oído tantas veces lo de «todo es determinista pero rara vez determinable».
Pero considerar al azar no nos lleva necesariamente al indeterminismo ni mucho menos, el azar es perfectametne compatible con el determinismo aunque suponga un handicap o «ruido» como le gusta decir a Neo.
Abrazos para ambos.
domingo 18 marzo, 2012 @ 7:02 pm
Estimado Miguel Ángel:
El primer párrafo (que está incluso separado de los demás) no se refiere específicamente a ese señor. Es un aviso a navegantes sobre los textos «divulgativos» que circulan por ahí en donde se hacen esas cosas y que tratan a los humanos como semidioses que crean la realidad cuando la observan.
lunes 19 marzo, 2012 @ 10:36 am
Querido amigo Miguel Angel:
Para negar por completo el azar no preciso de las variables ocultas. Me basta, como digo, con la consideración de que si algo puede atribuirse al azar, la ciencia no podrá decir nada sobre ello, por lo que resultaría inútil; en el mejor de los casos podría acotarse una parcela de la realidad y, renunciando a la ciencia en ella, dejarla al arbitrio del azar. La ciencia serviría sólo para el resto. Pero no tengo claro cómo podría ser porque escribo conforme lo pienso. ¿A qué campo pertenecerían sus límites? Y no es tontería esta pregunta porque me parece que nos lleva a una imposibilidad: Si el límite pertenece al azar, deberá estar dentro de él y requerirá otro límite al que sucederá lo mismo, convirtiendo en azar toda la realidad; si, por el contrario el límite es determinista, requerirá otro límite para el azar al que sucederá lo mismo, y así sucesivamente, de modo que toda la realidad será determinista. Es decir que no puede haber parcelas de azar en una realidad determinista y viceversa.
En tu segundo párrafo te refieres a mi idea de lo determinado y lo determinable. Mi intención al expresarla es argumentar a aquellos que, cuando no encuentran explicación a algo, renuncian a buscar y se conforman con atribuir al azar la causa. Un azar X no puede ser causa de nada Y. Podría ser -a priori- de Y, Z, T, etc., según alguna ley inexistente, porque si existiera, dejaría de ser azar. Y es evidente que la ciencia aún no es capaz de pronunciarse sobre muchas parcelas de la realidad. Por tanto estamos ante sucesos no determinables. Las causas pueden ser muchas. Al fin y al cabo, por poner algo sobre la mesa, hasta hace bien poco nada se sabía sobre la materia oscura y menos sobre la energía del mismo no-color. En estos momentos sabemos que el despiste es importante. Algo es algo; por lo menos conocemos algún inicio de nuestra ignorancia. ¿Y cuantos entes habrá así?: imposible saberlo. Sólo he querido demostrarte que los sucesos indeterminables existen (no intrínseca y necesariamente indeterminables; quizá algún día puedan ser determinados). La existencia de los determinados y por tanto determinables es obvia y no precisa explicación. Por tanto negar que han de existir leyes, entes, variables, constantes que desconocemos, que ignoramos el origen del Universo y sus límites, que intentamos resolver todo ello por medio de la ciencia y no del azar, que existe la posibilidad de que tanto los máximos como los mínimos componentes de la materia quizá nos estén vedados, es absolutamente irracional. Obviamente no lo conocemos todo y nunca lo conoceremos porque cada respuesta nos castiga con un montón de nuevas preguntas.
Ese «ruido» al que te refieres puedo admitirlo y explicármelo incluso como una forma de la realidad más ínfima. Me acojo, como digo no sé si en este o en otro artículo, a la dualidad onda-partícula que, a mi modesto y muy limitado entender, es una forma de decir o una forma de percibir. Sospecho que es, en realidad, sólo energía y que lo es en forma de onda. Lo que debe suceder es que esa onda es perceptible ocasionalmente como partícula y que admite el tratamiento físico-matemático de partícula hasta que revela su verdadera intimidad. Si a eso sumamos la historia de la física en la que todo se ha matematizado para partículas hasta finales del XIX o principios del XX; si consideramos que en nuestra realidad cotidiana las ondas son poco «evidentes», tenemos razones poderosas para comprender la situación.
Recibe toda mi consideración y afecto.
lunes 19 marzo, 2012 @ 8:59 pm
Mediando en la conversación entre Miguel Ángel y Tomás se podrían decir varias cosas:
-No es lo mismo azar que contingencia.
-Podemos confundir nuestra ignorancia o incapacidad con cierto nivel de azar.
-Un sistema totalmente azaroso del que puede salir cualquier cosa no es estudiable científicamente porque no es posible comprobar predicciones.
-Se puede hacer ciencia y modelos con un pequeño grado de azar. A veces este azar mide nuestra ignorancia sobre el sistema. A veces ese azar es despreciable o es ignorado.
-La capacidad de predicción de un modelo y su comprobación dependen de la aislabilidad del objeto de estudio.
-Se puede hacer estadística con cierto grado elevado de azar (sea por ignorancia o intrínseco si es que éste se da).
-Cuánto hay de azar real o ignorancia hay en un sistema choca con el grado desconocido del hecho ontológico o epistemológico. Quizás la MC tiene del primero y la ruleta del segundo.
-Cierto grado de azar puede no amplificarse y no tener efecto a largo plazo o gran escala.
-Cierto grado ínfimo de azar o de ruido puede amplificarse de tal modo que dé al traste con predicciones a largo plazo.
-Hay cosas que se han demostrado que son incomputables.
-El demiurgo de Laplace es imposible incluso suponiendo que sólo existe la Mecánica Clásica y ni haya caos determinista (el adjetivo determinista es parte del nombre técnico). No hay nada dentro del sistema (Universo) que permita esa computación, así que aunque todo fuera determinista (intrínsecamente), casi todo sería impredecible (gnoseológicamente).
-La RG es clásica y, sin embargo, predice las singularidades, de las que puede salir cualquier cosa. Podemos ignorar las singularidades de los agujeros negros, pero no la desnuda del Big Bang. Las teorías cuánticas de la gravedad eliminan las singularidades.
-No sabemos si la MC es una teoría definitiva que describa una realidad ontológica o si es sólo un modelo.
-No sabemos seguro si la MC mide lo que podemos conocer de los sistemas (debido a nuestra incompetencia) o si mide lo que ningún sistema de conocimiento o información puede «saber» sobre el microcosmos. No sabemos si esa «aletoriedad cuántica» es intrínseca o no (parece que sí).
-El valor esperado de los observables en MC destruye la «borrosidad» de la función de ondas para dar un valor fijo. La energía de transición de un electrón de un nivel a otro es proporcionada (a través de los autovalores) por la MC con una precisión inaudita. No es un valor que varíe azarosamente.
-No sabemos qué interpretación de la MC es válida, si lo son todas o no lo es ninguna conocida y está por ver si damos con la interpretación definitiva.
-No parece que haya posibilidad de crear experimentos que distingan entre interpretaciones de la MC. Parece algo indecidible.
-La interpretación de la MC no parece afectar a la realidad física, sólo a nuestra forma de pensar sobre ella.
-Ni el azar ni la MC garantizan el libre albedrío de los individuos, sólo la impredecibilidad (hasta cierto punto) de sus acciones. No es lo mismo poder elegir algo, que aleatoriamente algo elija por uno.
-No sabemos si hay algo más allá de la MC y si existe si lo podremos descubrir, tampoco sabemos si el método científico lo puede desvelar o no.
-No conocemos todos los límites impuestos a cualquier tipo de conocimiento por el Universo y su Física. No sabemos qué límites se han impuesto al conocimiento del ser humano y a su cerebro.
-No sabemos por qué las Matemáticas funcionan tan bien para describir el Universo.
-Una pregunta última que empiece con un por qué suele ser ilegítima porque presupone una intencionalidad. En ciencia es mejor empezar las preguntas con un cómo.
-El método científico tiene sus límites y tampoco sirve para contestar las preguntas últimas.
…
martes 20 marzo, 2012 @ 11:39 am
¡Caramba, Neo! Te has extendido tanto -comprimiéndolo todo- y en tanta profundidad para mis capacidades que no me atrevo a pronunciarme. Bueno, sí en forma global: Va a ser muy difícil no estar de acuerdo contigo. Pero me gustaría pormenorizar:
He empezado, pero me rindo. He borrado lo escrito. Tu comentario es inabarcable. Quizá mejor otro día, seleccionaré los que me parezca que deben ser aclarados.
Un cardial -también cordial, pero es que voy a tener que hacerme un electro tras el esfuerzo- saludo y gracias por tu escrito.
martes 20 marzo, 2012 @ 1:36 pm
Pues yo estoy tomando algunas notas del excelente 22 de Neo. Hay un punto que reconozco que me desarma por completo y es cuando dice «No sabemos que interpretación de la MC es válida, si lo son todas o no lo es ninguna conocida»; también es vertiginoso pensar que podemos encontrarnos con fenómenos que no podemos explicar usando el método científico, y lo que da vértigo es tener que recurrir a los otros tipos de conocimiento, lo que equivale a quedarnos sin explicación, ni modelo de explicación ni asomo alguno de racionalidad al que recurrir. Pero es posible que así sea y que la realidad última se muestre inalcanzable.
Enhorabuena por pilotar así de bien la nave, Neo.
martes 20 marzo, 2012 @ 9:10 pm
Estimado Miguel Ángel:
Sólo quisiera aclarar un punto por si se ha entendido mal. El método científico funciona bien siempre y cuando se tenga acceso experimental al fenómeno que se pretende explicar. Así que no podemos «encontrarnos» con fenómenos que no podemos explicar usando el método científico. El problema del método científico se da cuando hay (supuestos) fenómenos que están más allá de la experimentalidad. Cuestiones como otros universos, las cuerdas y demás están más allá de la ciencia. Incluso una teoría de partículas estándar puede que esté más allá de la comprobación porque no tengamos dinero para construir aceleradores más potentes.
miércoles 21 marzo, 2012 @ 10:43 am
Estimados Neo y Miguel Angel:
Es que podría escribirse todo un grueso volumen para desarrollar cuanto expone Neo en su 22. No recuerdo haber leído nada tan condensado.
Me gustaría empezar por aclarar ideas sobre el azar. Diría que el azar formaría, si es que existe, un subconjunto de lo contingente. Recuerdo haber dicho, no hace mucho, que lo posible es un conjunto que contiene dos subconjuntos disjuntos: uno es el de lo necesario y otro, el de lo contingente. Pues bien,lo azaroso sería un subconjunto de lo contingente.
Aunque pueda tomarse así, no es -para mí- azar que en el nº pi -3´14159…-, el 9 siga al 5. A esto suele llamarse aleatorio. Pues bien, este aleatorio habría de formar un subconjunto de lo necesario. Curiosamente ambos tienen en común lo siguiente: en este caso se trata de una aleatoriedad limitada a 10 números. Si consideramos un dado perfecto y una tirada absolutamente libre de toda influencia causal, el azar está limitado a 6 posibilidades. Pero en este último caso podemos usar el cálculo de probabilidades, lo que no sería correcto con los números irracionales. Podrá ser correcto hacer una estadística hasta, p. ej. la posición 1 millón, pero eso no puede servir de base para generalizar a toda la infinitud de sus cifras. Por tanto no podemos hacer el cálculo de una probabilidad, salvo que aceptemos el muy posible error.
Bueno, pues hasta otra. ¡Puff! Decídmelo si os canso.
Un abrazo a partes iguales.
miércoles 21 marzo, 2012 @ 9:58 pm
El número π no es aleatorio. Según la teoría de la computación un número es aleatorio si el tamaño mínimo del programa que genera n decimales de él es al menos de tamaño n. Básicamente en ese caso no podemos comprimir la información que contiene, la mejor manera de generar ese número es la propia secuencia de sus decimales.
El número π no cumple esa condición y por tanto no es aleatorio.
jueves 22 marzo, 2012 @ 8:47 am
Gracias estimado Neo. Se trata de que he empleado mal el concepto de aleatoriedad. Pero lo que quiero decir está claro: el 9 puede seguir inevitablemente al 5, pero no podemos predecirlo. He puesto ese ejemplo para simplificar y significar que no podemos saber, en una raíz que dé un irracional, el dígito que ocupará el lugar n, a pesar de que no puede ser mas que uno estrictamente determinado. Así, de momento no se me ocurre como llamarlo. El nombre debe significar determinado pero impredecible.
Un cordial saludo.
jueves 22 marzo, 2012 @ 9:26 am
Estimado Tomás:
Es que sí podemos predecir los decimales de π por eso la secuencia de sus dígitos no es aleatoria. Todos los programas para el cálculo de π hacen precisamente eso: calcular (predecir) qué número vendrá. De hecho cualquier programa que calcule cualquier número dará números que no sean aleatorios, como máximo pseudoaleatorios. La computación está pensada precisamente para evitar cualquier fuente de azar, de lo contrario los cálculos no serían fiables.
Sí se puede saber el dígito n de un número, aunque sea irracional. Hay programas que se dedican precisamente a eso y sólo calculan el decimal 1 millón, por ejemplo.
jueves 22 marzo, 2012 @ 10:18 am
Estoy totalmente de acuerdo con los puntos 1, 2 y 3. También con el 4, aunque merece una puntualización. En el momento que admitamos cualquier grado de azar, si tenemos conocimiento de él, o se acota y manifiesta, o no es buena ciencia.
También de acuerdo con el 5. El 6 es obligado sin excluir otras situaciones en las que no intervenga el azar; me estoy refiriendo al «Se puede hacer estadística…»
Hasta pronto.
jueves 22 marzo, 2012 @ 10:39 am
Estimado Neo:
¡Vaya! Acabo de escribir el 30 y me encuentro con el 29. Tengo el carrillo pi caliente por tus tortitas educativas. Sean bienvenidas si conducen hacia el conocimiento: «La letra con sangre entra».
Entonces te pregunto: ¿existe una expresión que, incluso para ese sólo número, me dé el dígito correspondiente a una posición cualquiera previamente elegida? Es que creo que no. ¿Será que hay que preparar un programa para que me dé sólo el correspondiente a la posición un millón, pero no sirve para la un millón uno?
Un abrazo. (Me he puesto un casco de moto).
jueves 22 marzo, 2012 @ 3:11 pm
Estimado Tomás:
No se preocupe, ese tipo de error es común. En cuanto al programa da igual, si tenemos uno que calcula un dígito específico es fácil crear otro que calcule cualquiera. Sea en este caso o en cualquier otro.
El problema es el tiempo de cálculo requerido, que crece conforme el decimal es más profundo.
viernes 23 marzo, 2012 @ 9:45 am
Bien, pues voy a poner otro ejemplo a ver si atino. Mi intención es usar la palabra azar para aquello que sea incausado o bien para aquella causa que pueda tener distintos e imprevisibles efectos no ateniéndose a ninguna ley, como se predica sucede en la desintegración del átomo, aunque haya una estadística que lo acoja. Sin embargo, aleatoriedad lo emplearía para lo caótico, p. ej. la posición en el plazo de un año de una molécula de N2 a la que hemos marcado para reconocerla. Ha de estar en algún sitio concreto, pero las variables son tantas y tan desconocidas las interacciones de los movimientos atmosféricos, que resulta imposible predecir tal posición.
Creo que otorgando yo el significado a lo que digo, se resuelve el problema. De todas formas estoy dispuesto a admitir otra palabra que designase mejor esa propiedad de determinado pero indeterminable.
Agradecido, Neo por tus aclaraciones.
viernes 23 marzo, 2012 @ 10:17 am
Volviendo al 22 de Neo, también estoy totalmente de acuerdo con los 7, 8 y 9; son naturales en la práctica del método científico y se tienen en cuenta a la hora de aceptar o no la exactitud de los datos y resultados.
En cuanto al 10, supongo que lo que digo en mi comentario anterior de la molécula de N2, estará incluido en uno de esos incomputables. Pero no creo que esta palabra sea sinónima del significado que doy a aleatorio. No estoy seguro.
Saludos.
viernes 23 marzo, 2012 @ 9:04 pm
Ese azar que menciona sobre la molécula de nitrógeno puede considerarse como tal. No es sólo las interacciones a las que está sometida, es un problema de aislabilidad. No podemos aislar un trozo de atmósfera del resto del Universo y el resto del Universo mete por tanto ruido en el sistema.
Todo depende de si es interesante la posición de tal molécula. Lo que nos interesa en general es la presión y temperatura. Éstas dependen de la colectividad y tienen un valor determinado independientemente del ruido de sus constituyentes.
Si ese ruido no se amplifica (como en el caos determinista) no importa demasiado.
Lo ideal seria reservar la palabra caótico para el caos determinista (efecto mariposa).
También hay procesos estocásticos. Y modelos que incorporan ese tipo azar. Si éste no es muy intenso se pueden calcular cosas.
sábado 24 marzo, 2012 @ 8:24 am
Bien, puedo aceptar caos para designar lo que media entre la posiciones inicial y final de la molécula; aunque no azar como dices al comienzo. Pero esto no podemos discutirlo pues va a ser difícil llegar a un acuerdo ya que tú expresas una ciencia práctica, real -«no podemos aislar un trozo de atmósfera»- y yo te hablo de una experiencia teórica, ideal, que sé imposible: por mucho que marque la molécula de N2 -haciéndola por ejemplo un isótopo único y estable-, vete a buscarla al cabo de un año, que dirían en mi tierra. Pero como sería posible saber dónde está en el instante siguiente de haberla soltado, y tras este lo mismo sucesivamente hasta totalizar el año, resulta teóricamente posible, pero absurdo en la práctica.
Entonces, ya tenemos unos cuantos conceptos a redefinir para el final: necesario, posible, contingente, azaroso, aleatorio y caótico. A ver qué sale.
sábado 24 marzo, 2012 @ 8:58 am
También estoy de acuerdo con el 11 -«El demiurgo de Laplace…», ¿como no si ni siquiera sabemos si el Universo es finito y ni aunque lo fuera?
En cuanto al 12, las singularidades de los agujeros negros nos son sencillamente desconocidas por no tener medios -y posiblemente nunca los tengamos- de averiguar algo de su interior -de todas formas yo creo que podrán hacerse supuestos matemáticos, si no se han hecho ya-. Pero lo del Big Bang ya es otra cosa. No digo que la teoría al uso esté equivocada, pero creo que pudo ser de otra forma. Por ejemplo una tremenda nube, quizá infinita -es que en esto nuestra ignorancia es total- que se comprime y, en un momento dado, sin llegar a la singularidad de un punto ni nada parecido, «rebota» y comienza una expansión que ahora continúa. Pienso que esto sería compatible con el fondo cósmico y con el alejamiento de las galaxias, haciendo innecesaria, además, la fase de inflación que ha tenido que ser supuesta «ad hoc». Pero mi incultura en MC no me permite entender la frase: «Las teorías cuánticas de la gravedad eliminan las singularidades»
Respecto al 13, creo que todas las teorías son modelos de la realidad. Porque se me hace que la realidad última siempre será inasible y por tanto nunca podremos estar seguros de que el modelo propuesto responda fielmente a ella. Al menos, la historia de la ciencia así lo ha venido demostrando hasta ahora.
Un saludo muy cordial y gracias por la paciencia.
lunes 26 marzo, 2012 @ 1:39 pm
Nuestras propias vidas son inherentes al azar y a la incertidumbre. Esta incertidumbre pueden resultarle muy molesta al lóbulo frontal izquierdo (previsor, ciéntífico y calculador) de hecho hay una amplia gama de trastornos mentales asociados a la sensación de falta de control, pero muy poética al derecho:
«..andar como un vagabundo,
sin rumbo fijo, sin meta,
a vueltas de veleta,
al soplo del viento al AZAR
…no me propongo DESTINO,
no quito puestos a nadie,
porque mi puesot es el aire,
como el olor del buen vino
…no dejo rastro ni huella,
por no ser ni soy recuerdo,
yo paso haciendo silencio,
sin ser esclavo del tiempo
Por límite el horizonte,
y por frontera la mar,
por no tener no tengo norte
y no se lo que es llegar»
De la canción «Andar» de Cecilia.
Abrazos
lunes 26 marzo, 2012 @ 1:50 pm
Con perdón, continúo: El 14: «No sabemos seguro si la MC…», está redactado de tal manera que conviene una discusión. Quizá podamos descartar el «debido a nuestra incompetencia», pero claro, no podemos saberlo. Otra cosa es si estamos ante lo que «ningún sistema de conocimiento o información puede saber sobre el microcosmos». En este caso el problema está en el sistema que no puede saber, o incluso en si nunca podrá haber un sistema que pueda saber.
Por otra parte está lo que radica en la realidad misma: «No sabemos si esa «aleatoriedad cuántica»…(parece que sí)». Sí, me temo que tiene todas las papeletas para ser así.
El tranquilizante modo (visto ahora) en que, de estudiantes, llegábamos al principio de incertidumbre ha dado un paso adelante y se nos muestra ahora como algo propio de lo más íntimo de la materia. Ante eso yo sólo puedo pensar que esta forma de la energía la percibimos así, pero nunca es así: siempre es onda y siempre tiene las propiedades de una onda. No existe la partícula; sólo nos parece o exhibe propiedades que la hacen parecer. Cuando a mis hijos les enseñaba el principio de exclusión de Pauli -en versión elemental- su mayor problema estaba en cómo pasaba un electrón de una capa a otra sin tiempo ni posición que mediara.
Les explicaba y me lo explicaba de esa manera: quedaba algo confuso, pero más admisible.
En resumen, que acepto irremediable y dolorosamente ese punto. ¡Con lo sencillo que sería un Universo de partículas, de pelotitas cada vez más pequeñas -sin pasarse- y ya está! Pero no. ¿Qué se le va a hacer?
El 15 me consuela absolutamente. Es mi preferido y, como hace Miguel Angel, bueno, mejor y lo siento: le voy a poner mentalmente un marco de oro. Y es que, si no fuera así -sin esa «precisión inaudita»-, imaginemos -perdón si digo una insensatez- que los estados pasasen al siguiente sin colapsar, con toda su aleatoriedad. Esta se iría multiplicando exponencialmente y no habría forma de predecir: el resultado final sería inevitablemente azaroso. Los acontecimientos no sólo no serían indeterminables; serían indeterminados en lo más íntimo de su ser. Cuando desease una información del ordenador podría salir cualquier cosa, o una mezcla de ellas. Si apretase la tecla de la A podría salirme cualquiera, apagarse el ordenador o hasta dar un saltito todo el teclado. Mucho mejor como está.
El 16, que tanto angustia a mi muy estimado Miguel Angel no me causa ningún desasosiego. En la historia de la ciencia, ante un progreso, como por ejemplo la mecánica newtoniana, una vez aceptado, parecía inamovible. Pero ya desde hace tiempo nos hemos dado cuenta de que las descripciones de la realidad son provisionales, como debe ser por las características del método científico. Siendo así, es obvio que habrán de tener, también diversas interpretaciones y que pueden ser válidas o no. Es el hombre quien juzga esa validez; no podemos olvidarnos de él, aunque esta es otra cuestión.
También de acuerdo en el 17. «Parece algo indecidible». Estamos en los límites del conocimiento y quizá de la experimentación en ese campo; al menos por ahora.
El 18 es de cajón. Tampoco creer en dios afecta mucho a la realidad. ¡Es tan terca!
El 19: «Ni el azar ni la MC…». Nada que objetar.
El 20 y el 21, que dan vértigo a mi querido amigo Miguel Angel, son «de obligado cumplimiento». Me atrevo a asegurar que, si algunos de esos límites no han llegado ya, desde luego han de llegar algún día. Por otra parte, ya ahora, el método científico no es aplicable a todo conocimiento. Por ejemplo, no podemos aplicarlos a averiguar cómo es un agujero negro en su interior. Y tienes razón, Miguel Angel, es muy posible que la realidad última sea inalcanzable.
22: «No sabemos por qué las matemáticas…». En efecto, así es. Yo quiero pensar en que son como miles de dialectos lógicos dentro de un idioma más general, por lo que nos dan muchas posibilidades y gran elasticidad para aplicarlas a cualquier fenómeno. Además, cuando algo no se acomoda, se inventa la matemática o la geometría más adecuada. Los ejemplos son muchos. Cuando se precisó, Newton y Leibniz idearon el cálculo diferencial e integral; en su momento se inventó la topología. Es decir que creamos, si no las tenemos ya, las herramientas matemáticas necesarias para tratar el fenómeno. Creo que puede ser la respuesta.
Aunque parezca poco relevante, el penúltimo punto también merece un marco de oro. ¿Por qué se produce la evolución? es una pregunta sin sentido. ¿Cómo se produce la evolución? es una cuestión que la ciencia, el método científico, está tratando de resolver utilizando muchos caminos distintos de investigación.
De la misma clase me parece «¿Por que hay algo en lugar de nada?». A mí, me parece absurda. Y otras muchas que, como dice Neo, comienzan de esa manera. Así, no debemos preguntarnos tampoco ¿por qué las matemáticas…?: ¡calcula y calla! Amen -humildemente-.
Y como despedida, el punto último, expone afirmaciones que ya había aceptado antes. Quizá quede lo de las preguntas últimas: no son de la incumbencia del método, ni puede tener capacidad para responderlas; además le son absolutamente ajenas.
Recibe, apreciado y apreciable Neo, mi más sincera admiración por haber sabido condensar tanta sabiduría y tan acertadamente en las pocas líneas de tu 22 que, como digo, merecerían ser desarrolladas muy extensamente. Y un gran abrazo para ti, amigo Miguel Angel.
lunes 26 marzo, 2012 @ 9:06 pm
Gracias por todo, apreciado Tomas.
Lo difícil sería explicar el asunto de las Matemáticas. Quizás ya estén de algún modo embebidas en la estructura de la realidad.