Las abejas saben sumar y restar
Dos estudios recientes analizan las capacidades aritméticas de las abejas.

|
La habilidad de realizar matemáticas básicas fue fundamental para el florecimiento de sociedades humanas históricas. Ya los egipcios y babilonios usaban la aritmética hace 4000 años.
Desde los tiempos de Platón los filósofos han debatido si las Matemáticas existen o preexisten fuera de la mente de los humanos. Físicos y matemáticos dialogan sobre la belleza de las mismas y si esa belleza determina la Física o si sólo son un lenguaje que describe la realidad.
Creemos que hacer cálculos matemáticos es algo exclusivamente humano, aunque haya culturas humanas que sólo cuenten hasta tres. Pero desde hace décadas se sabe que algunos pájaros y otros animales pueden contar.
Ahora se ha descubierto que las abejas no sólo saben también saben contar, sino que son capaces de realizar cálculos matemáticos sencillos. El resultado es un tanto sorprendente, pues se asumía que un cerebro tan pequeño como el de las abejas no sería capaz de realizar semejante proeza. El resultado expande, por tanto, nuestra comprensión de la relación que existe entre el tamaño del cerebro y sus capacidades.
En estudios previos ya se había demostrado la capacidad de las abejas de contar hasta cinco. Además, podían elegir el grupo más grande o el más pequeño en función de las necesidades o incluso elegir el cero (conjunto vacío) entre otros cuando habían sido entrenadas para elegir el más pequeño.
Esto puede ser realizado si se entiende el concepto de número, como hacen los humanos, pero también de un modo automático mediante la corteza visual de estos insectos de tal modo que requiera la mínima potencia computacional.
Hace unas pocas semanas un equipo de investigadores de Queen Mary University of London publicaba un estudio en el que emulaban estas cualidades de las abejas mediante la simulación de su red neuronal.
El cerebro de las abejas es muy pequeño y cuenta con pocas neuronas (sólo un millón) comparado con el cerebro de, por ejemplo, un humano. Pero esta simpleza permitió a estos investigadores simularlo en un ordenador.
Comprobaron que este pequeño cerebro simulado podía contra pequeñas cantidades mediante una simple inspección visual, tal y como hacer la abejas. Esto explicaría las capacidades matemáticas de estos insectos de una manera sencilla señalando que estas habilidades, en realidad, se pueden realizar de un modo sencillo con escasa capacidad de cómputo. Así que la inteligencia de las abejas y otros animales podría estar mediada por un pequeño número de neuronas, siempre y cuando estén conectadas entre sí de la manera adecuada. De este modo, no se requeriría grandes cerebros para este tipo de tareas, sino que pequeños circuitos neuronales pueden ser acomodados para realizarlas.
Pero este resultado necesitará ser actualizado, si es que es posible, debido a un nuevo estudio que nos dice que las habilidades aritméticas de las abejas son todavía más sofisticadas que lo que se creía.
Ahora, otro equipo de investigadores, esta vez australianos y franceses, ha demostrado que las abejas parecen comprender el concepto de cero y de realizar operaciones sencillas de adición y sustracción.
Hay cierto debate sobre si algunos animales puede aprender o no habilidades numéricas complejas. Muchas especies pueden entender la diferencia entre distintas cantidades y usarlo en su forrajeo, su toma de decisiones o para resolver problemas. Pero las habilidades de cálculo más sofisticas como las operaciones aritméticas requieren de un nivel de procesamiento más sofisticado. En estudios previos se pudo comprobar que algunos pájaros, los bebés, los primates o incluso las arañas pueden sumar y/o restar.
Resolver problemas matemáticos sencillos requieren de cierto nivel de sofisticación y de habilidades cognitivas que permitan manipular mentalmente números, manejar a largo plazo ciertas reglas y ordenar todo ello en una memoria de trabajo.
En los experimentos que estos investigadores han realizado se demuestra que las abejas pueden ser entrenadas para reconocer colores como representaciones simbólicas de la suma y la resta y, además, que pueden usar esa información para resolver problemas aritméticos.
«Necesitas ser capaz de mantener las reglas de sumar y restar en tu memoria a largo plazo mientras que mentalmente manipulas un conjunto dado de números en tu memoria a corto plazo», dice Adrian Dyer (University in Melbourne).
«Por encima de todo esto, nuestras abejas, además, usaron su memoria a corto plazo para resolver problemas aritméticos y aprendieron a reconocer los signos de más o menos como conceptos abstractos en lugar de ser simples ayudas visuales», mantiene Dyer. Añade que sus hallazgos sugieren que las facultades cognitivas orientadas hacia una matemática relativamente avanzada pueden ser encontradas en la naturaleza en una mucha más amplia gama de animales que lo que previamente se había sospechado.
Sin embargo, al final llega a una conclusión parecida a la de los investigadores de Queen Mary University of London, al decir que si las matemáticas no requieren de un cerebro masivo, entonces posiblemente hay nuevas vías de incorporar interacciones entre reglas a largo plazo y memoria de trabajo en el diseño de la inteligencia artificial (IA) de tal modo que se mejore la eficacia de su aprendizaje en este tipo de sistemas.
|
Las abejas del estudio recibían una recompensa en forma de agua azucarada cuando realizaban la elección adecuada y una solución amarga de quinina cuando su elección era incorrecta.
Como las abejas suelen volver a las localizaciones en las que hay buenas fuentes de néctar, estas solían volver al montaje experimental para conseguir más comida y, de paso, aprender a sumar y restar.
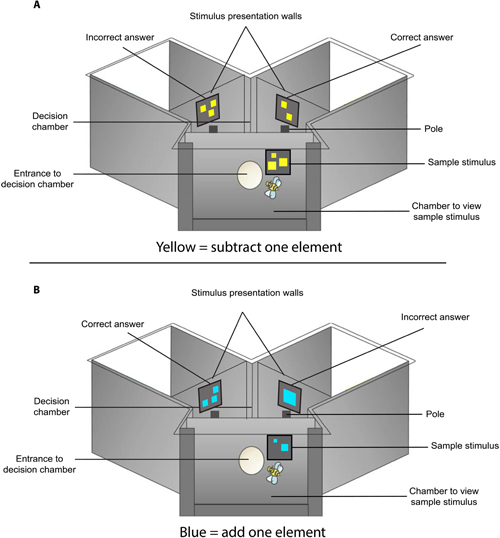
Al entrar veían un conjunto de elementos de una a cinco formas distintas. Las formas era o bien azules que venía a significar el símbolo de suma o amarillo, que simbolizaba el signo de sustracción.
Una vez habían visto el número inicial, la abeja volaba a través de un agujero hacia la cámara de decisión en donde tenía que elegir entre volar a la izquierda o derecha. Un lado correspondía al resultado correcto de la operación aritmética y el otro al incorrecto, con sus sendas disoluciones azucarada y amarga.
Al principio las abejas realizaban elecciones al azar, pero al cabo de 100 intentos, lo que les llevaba de 4 a 7 horas, las abejas aprendían que azul significaba +1 y amarillo -1. Después conseguían aplicar estas reglas de suma y resta a otros números.
«Nuestros resultados muestran que la compresión de símbolos matemáticos complejos como un lenguaje es algo que muchos cerebros pueden posiblemente conseguir y ayuda a explicar cómo muchas culturas humanas desarrollaron por separado habilidades numéricas», dice Scarlett Howard (University Melbourne).
Estos estudios tienen implicaciones en IA porque podría aumentar la eficiencia de robots autónomos que necesiten descansar sobre algoritmos robustos y computacionalmente eficientes que no consuman muchos recursos. Particularmente, podría ser interesante su aplicación en el aprendizaje rápido.
Copyleft: atribuir con enlace a http://neofronteras.com
Fuentes y referencias:
Artículo original I.
Artículo original II.
Esquema: Scarlett R. Howard, Aurore Avarguès-Weber, Jair E. Garcia, Andrew D. Greentree y Adrian G. Dyer.
Foto: Lars Chittka.
10 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





lunes 11 febrero, 2019 @ 9:49 am
Bueno, seguimos sin tener clara la distinción entre cerebro y mente (si es que la hay), aunque barruntamos que es algo así como software y hardware, sobre todo en el sentido del soporte lógico como intangible y el soporte físico como muy tangible y mucho tangible. La capacidad de sorpresa (que no de asombro, o al menos para mis pedestres cánones) a veces es directamente proporcional a nuestra ignorancia.
Por supuesto en todo este debate paira el prejuicio puro y duro antropopiteco, esto es nuestro y los seres inferiores no deberían tenerlo, si se suspende tal prejuicio la cosa pierde bastante de asombrosa porque devuelve el foco adonde realmente está: nosotros. No las abejas, que evolutivamente tiene todo el sentido (y hasta la necesidad) que tengan capacidades algebraicas y obviamente náuticas.
Ahora, todos estos estudios más bien por donde abren vía de agua, o al menos así lo veo yo, es en que las matemáticas son «reales», o al menos tan reales como la fuerza de la gravedad. Esas teorías tan cuasisolipsistas que les atribuyen mucho de humanas me temo que están recibiendo palo tras palo. C’est la science, funciona así.
Pero bueno, siempre se puede meter todo en el mismo saco. A fin de cuentas, himenópteros y primates somos animalia y heredamos sistema nervioso, entre otras cosas. Ahora, yo mi dinero no lo apostaría por aquí.
lunes 11 febrero, 2019 @ 1:05 pm
Las matemáticas, o al menos una parte importantísima de ellas, no son tan reales como la fuerza de la gravedad porque, para empezar, pueden desarrollarse a partir de axiomas que nada tengan que ver con lo real. Como dijo Einstein «Cuando las leyes matemáticas se refieren a la realidad, no son exactas; cuando son exactas, no se refieren a la realidad». Pero, a mi entender, lo verdaderamente exacto en sí mismo, lo percibamos o no, es la realidad. Es decir, la realidad es exactamente igual a sí misma. Las matemáticas pueden describir la realidad y otras veces ni lo pretenden, sino que tienen su finalidad en sí mismas. A veces como el arte, a veces como el lenguaje.
lunes 11 febrero, 2019 @ 5:36 pm
Es difícil explicarse. Por un lado, podríamos inventarnos leyes físicas basadas en axiomas que no existen en el mundo real (a veces lo hacemos), pero la física es una ciencia empírica, y no es sostenible en el tiempo esta aproximación. En cambio las matemáticas no necesitan pasar por el juez experimental de la misma forma, de ahí que su nivel de desbarre sea, a estas alturas que estamos, de alucina con el videojuego. Pero lo que intentaba definir es que, si bien la física está pegada a la realidad en el sentido que busca explicar y estructurar el mundo tal y como nuestros sentidos (biológicos y expadidos instrumentalmente) lo perciben, las matemáticas quizá también, aunque no de una forma tan cruda, digamos. En ese sentido, «contar» es una realidad exterior y no una interpretación cultural, aunque debatir en estos términos es un patinete total.
Siempre ha habido gente que más o menos viene defendiendo que las matemáticas tienen una carga cultural (o biocultural, si queremos ponernos exquisitos) mucho más fuerte que la física, signifique esto lo que signifique e implique lo que implique. Es, digamos, poner las matemáticas más cerca de la liga del arte (escultura, música, poesía, tecnología, mitología, etc.) que de la física, en el sentido que «sale menos» hacia el exterior de la realidad desde nuestra burbuja de autoconsciencia humana de lo que la física lo hace. Si es que tiene sentido algo de todo esto.
En mi opinión, estos estudios van anulando este punto de vista como falso (con las consecuencias que eso implique, que obviamente ignoro). Las matemáticas tendrían la misma base sobre la realidad que la física, en el sentido de reglas del cosmos, quizá en otra capa o como quieras verlo. Que haya estructuras matemáticas que no tengan correspondencia (que no puedan existir) en el mundo real tampoco es muy distinto de unas ecuaciones newtonianas con otro valor de G u otros términos (a fin de cuentas, son herramientas matemáticas).
martes 12 febrero, 2019 @ 8:58 am
Quizá no estemos hablando exactamente de lo mismo, pero puedo discrepar de alguna de tus afirmaciones. Dices que «las matemáticas no necesitan pasar por el juez experimental». No es que no lo necesiten; es que no podrían. Una vez establecido el sistema axiomático, todo las propiedades que vayamos descubriendo son tautologías: eran consecuencias necesarias, solo que aún no habíamos caído en ellas. Además, las ciencias precisan el método científico que significa experimentación tan exhaustiva como se pueda y lo que yo llamo el salto al vacío de la generalización, lo cual no puede hacerse en matemáticas. En ellas precisas una demostración abstracta usando la misma axiomática, por lo que el salto a la generalización no es posible.
En cuento a la comparación del valor de G con herramientas matemáticas y, lo más importante, la «invención» de campos, también se distinguen en que precisan el método científico, mientras que ello no sucede en las matemáticas.
Por último, las verdades científicas, son provisionales, mientras que las verdades matemáticas son realmente verdades indiscutibles si se ha demostrado correctamente en su contexto.
miércoles 13 febrero, 2019 @ 2:19 am
Por eso algunos pensamos que habría que excluir el concepto de teorema del campo de la Física y hablar solamente de teoremas matemáticos.
miércoles 13 febrero, 2019 @ 2:22 am
Es decir, en vez de teoremas de la Física, deberíamos hablar de «leyes».
miércoles 13 febrero, 2019 @ 9:32 am
Creo que estoy de acuerdo en lo que dices y, diría, que también habría que añadir el calificativo de «principio», una vez que algo es deducible. Pudo ser «principio» cuando no había explicación, pero una vez que puede explicarse por conocimientos posteriores, deja de serlo. Pienso que algunas veces se mantiene el calificativo por tradición.
miércoles 13 febrero, 2019 @ 10:03 am
Quería decir, en lenguaje pedestre, que tal como tenemos montado el tinglado, las matemáticas no pasan por el juez experimental, aunque es interesante que esto empieza a matizarse de una forma muy incómoda debido a la brutal complejidad que han alcanzado. Pero lo que no supe explicar es que el hecho de que las matemáticas describan posibilidades que no tienen existencia real se debe exclusivamente a esto, que no desechan porque aunque sepamos (o pensemos) tal cosa sigue siendo útil, en cambio un modelo físico vapuleado por la realidad poca utilidad devuelve para el consumo de recursos. Pero esto también es debido por la utilidad que le damos a las matemáticas o a la física. En realidad, se podría decir que la física es la aplicación de las matemáticas, o nuestro intento de, al mundo real. Las matemáticas no se les pide ocuparse del mundo real, tal como lo entendemos físicamente (es de suponer que para un matemático tan real de la realidad matemática es esto como aquello).
Normalmente discrepamos en definiciones o cómo entendemos las definiciones, no en el fondo. Hay otra cierta obsesión con lo de «verdad», y sus apellidos nobiliarios, «duquesa del absoluto», «marquesa de lo definitivo», «princesa de lo inamovible». Veamos, tenemos verdades firmes y sólidas, no se van a mover ya, insisto, sabemos que la mecánica newtoniana es válida en su dominio de definición, eso no va a cambiar ni ahora ni nunca, y sí, podría suceder que su dominio de definición se vea quizá más achicado en el futuro, no se puede descartar, al fin y al cabo es una verdad incompleta, pero eso, y no estoy haciendo de tahúr, no es porque tengamos una verdad líquida y fluida que se va a mover bajo nuestros pies, es porque hemos puesto los pies fuera de la plataforma que tampoco es tan estrecha.
El problema, claro, está en la palabra «verdad». Una «verdad» matemática sólo significa que es autoconsistente consigo misma dentro de un entorno lógico, no es el tipo de «verdad» que busca el espíritu humano porque que el análisis esté bien o mal es importante, pero como decimos no tiene por qué corresponderse con la realidad. Esto nos llevaría a resbalar por una pendiente sin retorno. Las «verdades» empíricas sí son reales, en el sentido de corresponderse con la ídem, sucede que más que provisionales son incompletas, y nos cuesta mucho acotarlas, pero es que esto sucede, en mi opinión siempre, porque aparte de no saber acotar nuestras bases, planteamos preguntas incorrectas que sólo pueden ser contestadas cuando se han reformulado por completo, y entonces la pregunta original ya ni tiene sentido, y la «verdad» así suministrada ni puede responderla.
Por eso las «verdades» matemáticas no tienen nada que ver con las «científicas». Las primeras son la constatación de la no falsedad de un enunciado, las segundas son inaprensibles un poco como el principio de incertidumbre: si las concretamos lo suficiente para apaciguar nuestras ansiedades culturales, no somos capaces de discernir los límites para aplicarlas, si somos capaces de entenderlas casi tal cual un enunciado matemático, entonces no nos sirven para nada (cultural) porque no tienen sentido (como verdades).
Vamos, que si tenemos un problema con la realidad mejor como suelo decir moverse por certezas o probabilidades que por verdades.
jueves 14 febrero, 2019 @ 9:48 am
De acuerdo. Una verdad matemática o lógica no es lo mismo que una verdad científica o de interpretación de la realidad. En la primera basta que el resultado sea correctamente deducido de los axiomas, independientemente de si estos tienen algo que ver con la realidad. En el caso científico, aunque participe alguna axiomática, le queda la «prueba del algodón», tan popularizada como frase bien hallada.
viernes 15 febrero, 2019 @ 10:16 am
Es que, pensemos, una «verdad» científica, el valor de la constante c y su inviolabilidad. La tenemos bastante bien acotada, sabemos que en nuestro universo, aquí y ahora, podemos agarrarnos razonablemente a ella como pilar firme, si alguna vez se llega a soslayar «aquí y ahora» tendrá que ser de forma que no se puede violar ninguno de los cuadros físicos harto asentados (porque además lo estaríamos constatando ya), si en el pasado o en el futuro cambia, lo será porque las leyes del universo forzosamente cambian en esos escenarios (si c dependiese de la expansión, esto implica que muchas leyes son variables en el tiempo, p.ej.).
¿Nos sirve culturalmente para algo el saber esto? En último término evidentemente sí, como logro de la mente humana, pero para dirimir esta disputa cultural de hoy, ayer o mañana, evidentemente para nada.