NeoFronteras

La introducción en el dilema del prisionero de jugadores deshonestos que tratan de ocultar sus intenciones sin ser desertores puros puede afectar a la competición entre cooperadores y desertores de una manera inesperada.

Desde que unas células individuales decidieron de alguna manera cooperar para formar seres pluricelulares la cooperación no ha abandonado este mundo. Ni siquiera está ausente en la competición entre especies, pues algunas deciden cooperar en relaciones simbióticas para así prosperar. Además, hay animales sociales que cooperan entre sí a un nivel tan elevado, como las hormigas o las abejas, que incluso algunos de sus individuos no se reproducen. El individualismo salvaje darwiniano predicado por algunos neoliberales no es la realidad única en la Naturaleza.
Hay muchos ejemplos de mamíferos que cooperan entre sí, pero el ejemplo más obvio es el del ser humano. Los humanos somos animales sociales que cooperamos entre nosotros, pero no siempre es así. De vez en cuando todos hemos podido comprobar que algunos humanos tienen comportamientos desohonestos, falsos o fraudulentos para así conseguir una posición de ventaja. Este tipo de comportamientos tienen recompensa en un mundo en el que la cooperación es muy elevada. Y, por tanto, la tentación del comportamiento egoísta es fuerte. Pero si todos fueran deshonestos las ventajas de serlo desparecerían. Así que las sociedades tienen que promover la cooperación castigando a quienes tienen mal comportamiento para así fomentar dicha cooperación y que esta no se venga abajo.
El problema es cómo al principio surge evolutivamente la cooperación si cualquier comportamiento deshonesto la destruiría. Para explicar este enigma los investigadores de este aspecto social se valen de diversos modelos, incluidos los matemáticos. Un modelo típico es el dilema del prisionero.
El dilema del prisionero fue descubierto por Merrill Flood y Melvin Dresher en 1950 mientras que trabajaban en RAND. Trata de dos ladrones a los que captura la policía por cometer un delito, pero sobre los que no tienen pruebas concluyentes a no ser que alguno confiese. Se les interroga por separado y se les ofrece un trato. Si uno de ellos culpa al compañero saldrá libre y el otro irá un año a la cárcel siempre y cuando éste otro no le delate. Si ambos se callan (cada uno coopera, en el lenguaje de la teoría de juegos) ambos van un mes a la cárcel, pero si ambos hablan (cada uno deserta, en el lenguaje de la teoría de juegos) van tres meses a prisión. Es un juego que no es de suma cero. El problema es que los compinches no se pueden comunicarse entre sí y el “juego” es a una sola mano o jugada.
El dilema del prisionero no tiene solución racional. Es decir, no hay una estrategia tomada de modo racional que su adopción no conlleve al arrepentimiento a posteriori al final del juego por haber tomado esa decisión. Lo más racional parece que es desertar, pero en ese caso ambos van a la cárcel por más tiempo que si hubieran cooperado. Pero si uno coopera se arriesga a que el otro no lo haga.
Sin embargo, cuando el dilema del prisionero se juega iteradamente pueden aparecer diversas estrategias ganadoras. Naturalmente, se puede eliminar la figura de los compinches e introducir en su lugar agentes que juegan a diversas versiones del dilema. Se pueden ir cambiando las puntuaciones del dilema para tener distintos valores y ver cómo eso afecta a las distintas estrategias, cómo evoluciona el fraude, cómo de fácil se detecta a los desertores o cómo pueden coexistir cooperación y deserción.
Ahora Attila Szolnoki (Academia Húngara de ciencias), Matjaž Perc (Universidad de Maribor) y King Abdulaziz (Universidad de Jeddah) publican en The New Journal of Physics un nuevo estudio sobre este asunto en el que emplean el dilema del prisionero.
Introdujeron en su modelo computacional tres estrategias: cooperación, deserción pura y cierto nivel de comportamiento deshonesto sin llegar a la deserción pura. Además, dispusieron de una distribución espacial para la expansión de las interacciones entre agentes con distinta estrategia.
En las simulaciones que se han hecho sobre este asunto se observa que el alto costo de ser un desertor juega en contra de los deshonestos, lo que fomenta la cooperación. Este tipo de resultado se puede calificar de intuitivos. Pero no siempre es así.
Estos investigadores han encontrado que la introducción cierta estrategia deshonesta en el juego, en concreto la existencia de jugadores deshonestos que tratan de ocultar sus intenciones, puede afectar a la competición entre cooperadores y desertores de una manera inesperada. No necesariamente cuanto mejor sea la detección de los desertores por parte de los cooperantes mejoran las condiciones para que aparezca evolutivamente la cooperación. Si el costo de ocultar las malas intenciones es moderado, entonces el coste extra de detectar a los deshonestos permite la existencia de un mayor nivel de deserción.
Aunque al final el alto coste del comportamiento deshonesto daña a los desertores, a corto plazo les beneficia porque los desertores natos o puros son dañados mucho más y son los primeros en salir del juego. Mientras tanto, los jugadores con cierto nivel de comportamiento fraudulento pueden coexistir con los demás y sólo salen del juego cuando el coste de ser deshonesto es muy alto. Si este es el caso entonces sólo quedan cooperadores.
Uno esperaría que si se aumenta la probabilidad de encontrar a los deshonestos se fomenta la cooperación al encontrar más desertores puros, pero no siempre es así. Ha sido inesperado encontrar que, aunque un alto nivel de detección consigue eliminar a los desertores puros, la competición entre desertores puros y desertores deshonestos beneficia a los segundos. Incluso una baja probabilidad de detección puede ser una buena estrategia para los cooperativos.
Según los investigadores estos resultados contraintuitivos provienen de patrones espaciales autoorganizativos. Las interacciones entre las tres estrategias llevan a la emergencia de ciclos en ciertas regiones o dominios en los que domina una estrategia sobre las demás dependiendo de las condiciones y del tiempo de simulación, dominios que están separados por transiciones de fase.
Encontraron además grandes extensiones del espacio de parámetros en las que las tres estrategias pueden coexistir.
Perc sugiere que el hallazgo arroja luz sobre la importancia de los ciclos de dominancia, que probablemente están más extendidos en la vida real de lo que se presupone.

En estas tomas mostradas secuencialmente se muestra el ciclo de dominancia que emerge durante la simulación que incluyen (arriba a la izquierda) desertores puros (en rojo) a otros (arriba a la derecha y abajo a la izquierda) dominados por cooperadores (en azul) a otro (abajo a la derecha) dominado por desertores deshonestos (en verde). Fuente: Szolnoki y Perc.

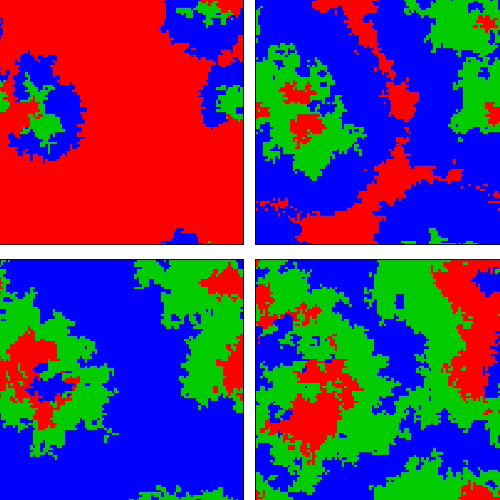
Los ciclos de dominancia de coexistencia de estrategia pueden terminar porque una de las estrategias se extingue o porque hay fluctuaciones divergentes en la amplitud de las oscilaciones.
Hasta ahora el tema de las transiciones de fase se ha venido estudiando en la Física Estadística y aplicado a los materiales de estado sólido o a la Física de Estado Condensado. Pero este estudio muestra un bonito ejemplo, según Szolnoki, de que el concepto se puede aplicar a otros sistemas complejos, en particular a sistemas sociales y biológicos. Aplicando dichos conceptos a estos otros sistemas se observan comportamientos fascinantes que no se habían visto en los casos tradicionales de la Física Estadística.
Este estudio muestra la oculta y compleja evolución de la deserción y gracias a ello proporciona pistas sobre dilemas sociales. Además resalta la posibilidad de que aparezcan consecuencias inesperadas o contraintuitivas cuando compiten estrategias sofisticadas en ciclos de dominancia.
Los investigadores esperan que este estudio inspire otros futuros en donde se investigue el papel de las estrategias de engaño, tanto en juegos como en la cooperación humana.

Copyleft: atribuir con enlace a http://neofronteras.com/?p=4537

Fuentes y referencias:
Artículo original
Copia artículo original.