NeoFronteras

Un nuevo protocolo podría permitir a los bancos la creación de billetes cuánticos infalsificables incluso para el propio banco.

Las raíces de la criptografía cuántica datan de la década de los sesenta, cuando Stephen Wiesner, un estudiante de doctorado en la Universidad de Columbia, intentó publicar sus ideas del dinero cuántico de clave pública imposible de falsificar.
Esta idea era tan avanzada para su tiempo que difícilmente alguien entendió el potencial de la misma, por lo que no se hizo más investigación al respecto.
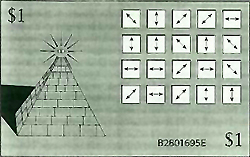
En la mente de este científico, un billete de dólar debería de contener 20 trampas de luz, pequeños dispositivos capaces de almacenar un fotón cada uno. Cada billete estaría identificado además por un número de serie único.
Las trampas de luz serían rellenadas con 20 fotones que tuvieran el estado de polarización dispuesto al azar en una disposición que sólo el banco (presumiblemente un banco central) conocería. Sólo podrían leerse (dejarlos escapar) y restaurarlos (reintroducirlos en las trampas) por el banco que supiera la exacta secuencia de filtros polarizadores necesarios para poder leer este «número de serie cuántico».
La idea central es que el banco pueda crea estados cuánticos que se puedan verificar, pero que nadie, excepto quizás el propio banco, puede clonar o falsificar. En teoría, como los estados cuánticos son imposibles de copiar, no se podría falsificar un billete de este tipo, pero alguien que deseara comprobar la autenticidad del billete tendría que llevarlo al banco en cuestión.
Aunque la idea es brillante nadie ha tenido éxito, hasta el momento, en la construcción física de una trampa de fotones lo suficientemente robusta, por lo que el concepto no es más que un problema académico. Esto no impide que desde el punto de vista teórico se siga investigando al respecto, sobre todo en el perfeccionamiento de los protocolos implicados. Además, la idea de Wiesner ha servido en los últimos años de inspiración para la criptografía cuántica.
Ahora, unos investigadores del MIT introducen unos protocolos “libres de colisiones” con los cuales ni siquiera el banco podría preparar copias idénticas de dinero cuántico, a diferencia de otros sistema propuestos con anterioridad.
El principal problema es que si asumimos el concepto de que el banco conoce la configuración de cada billete (aunque sea secreta) alguna organización criminal podría hacerse con la información y dedicarse a la fabricación cuántica de billetes. La seguridad del sistema residiría en la dificultad de hacerse con dicha descripción secreta.
Pero la creación de billetes cuánticos que ni los bancos puedan copiar ha resultado más difícil de lo pensado. Además, sería también interesante conseguir un billete cuya autenticidad pudiera ser comprobada por cualquiera sin necesidad de ir al banco emisor.
Se necesitaría, por tanto, alguna técnica asimétrica que permitiera al banco crear un dinero cuántico incopiable sobre el que cualquiera pudiera saber si es falso o no. Algo similar a este concepto se da en el sistema criptográfico de clave pública RSA, que se basa en la dificultad de factorizar números muy grandes y en la facilidad de multiplicarlos.
En el sistema RSA hay una clave pública para cada destinatario que conoce todo el mundo, así que todo el mundo puede cifrar, pero sólo el dueño de la clave privada puede descifrar los mensajes que recibe cifrados con su clave pública. Este sistema de cifrado no requiere de ningún sistema cuántico y basta un ordenador digital, tanto para cifrar como para descifrar, pero no hay computador lo suficientemente potente que pueda quebrar el sistema. Es el sistema que usted utiliza para conectarse a su banco por Internet. La idea sería crear un sistema asimétrico similar para el caso del dinero cuántico.
Andrew Lutomirski y su equipo del MIT sugieren un nuevo tipo de dinero cuántico al que denominan «libre de colisiones». La idea se basa en un estado cuántico diferente para este tipo de dinero.
Este estado es una superposición de muchísimos términos no relacionados entre sí y es creado por una superposición igualmente grande de medidas. Esto garantizaría que ni el banco podría reproducir el mismo estado en un plazo razonable de tiempo. Además, la autenticidad de cada billete se podría comprobar fácilmente con un algoritmo basado en cadenas de Markov.
Sin embargo, los autores del artículo no han podido proporcionar una demostración de que el sistema está totalmente libre de colisiones. El sistema requiere un pequeño acto de fe como el que se requirió cuando se introdujo RSA por primera vez.
Todo sistema basado en la imposibilidad de resolver un problema matemático en tiempo polinómico con un ordenador convencional puede ser resuelto rápidamente con un ordenador cuántico. Esto se ha demostrado para el caso de la factorización de números grandes. Así que puede ser que en el colmo de los colmos cuánticos el futuro dinero cuántico libre de colisiones sea finalmente falsificado gracias a futuros ordenadores cuánticos. Por cierto, si tales ordenadores se crean el primero en caer sería precisamente RSA.

Copyleft: atribuir con enlace a http://neofronteras.com/?p=2955

Fuentes y referencias:
Artículo en ArXiv
U. Klagenfurt.
MIT.