Sobre la belleza de las Matemáticas
Unos psicólogos tratan de estudiar la belleza de las ecuaciones matemáticas.
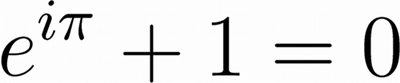
|
Siempre nos ha parecido difícil definir la belleza, pero desde la época de Platón dotamos a la misma de una cualidad especial, casi externa a la de los individuos que la experimentan. Pero ese placer que experimentamos al contemplar la belleza es puramente psicológico.
La variedad de objetos, personas o situaciones que podemos encontrar bellas es muy amplia. Incluso las cosas tristes o dolorosas pueden ser bellas en determinados contextos. No siempre la belleza está ligada a la felicidad o a la alegría.
Casi todo el mundo, eso sí, encuentra bonitas determinadas canciones, pero esto se debe también a que estamos muy impregnados de música por todos lados. El problema es que para los no iniciados quizás no les parezca bella una partida de ajedrez o una ecuación matemática.
Para los que estamos metidos en el mundo de las Matemáticas unas ecuaciones nos parecen más bellas que otras, incluso algún que otro físico famoso se guió en su día bajo consideraciones estéticas para alcanzar la expresión de una teoría con fórmulas matemáticas.
La cuestión es si esto se puede medir de alguna manera y si los gustos sobre ecuaciones son universales o si dependen de cada cual.
Semir Zeki (University College London) y sus colaboradores se propusieron medir precisamente eso gracias a un sistema de resonancia magnética nuclear funcional. Al parecer, la actividad cerebral de un matemático contemplando fórmulas es muy similar a la de la gente cuando contempla un cuadro de un gran maestro o escucha una obra cubre de la música.
Estos investigadores sometieron a 16 matemáticos a un test en el que tenían que calificar la belleza de 60 ecuaciones matemáticas. Labor que tuvieron que repetir dos semanas más tarde, pero esta vez con un sistema de resonancia magnética nuclear funcional vigilando su actividad cerebral.
Comprobaron que cuanto más supuestamente bella era una ecuación, más activo estaba el campo A1 del córtex orbitofrontal medio.
El córtex orbitofrontal medio es una región asociada con las emociones y se ha podido demostrar en estudios previos que el campo A1 tiene que ver con las respuestas emocionales a la belleza visual o auditiva.
En un principio no se esperaría este resultado, pues la belleza matemática de una ecuación provendría de una fuente intelectual más profunda y el campo A1 parece o parecía más relacionado con aspectos visuales o acústicos más primarios y, por tanto, más basados en la percepción. Pero, a raíz de los resultados, los investigadores sugieren que el campo A1 sí que es sensible a la belleza matemática.
El problema es cómo desligar el efecto de la cultura sobre la percepción de la belleza. Quizás los matemáticos crean que tal ecuación u otra es más bella porque a la hora de aprender matemáticas así se lo han dicho. El concepto de belleza de una ecuación sería, por tanto, algo aprendido.
Esto representa el mismo problema que en el caso de si alguien no instruido en música clásica puede apreciar o no la belleza de determinada sinfonía.
Para intentar solventar este problema los investigadores mostraron las mismas ecuaciones a personas que no eran matemáticos. Comprobaron que había menos respuesta emocional en su actividad cerebral. Incluso alguna persona no mostró respuesta emocional alguna. Pero, incluso sin entender las ecuaciones, algunos otros encontraron belleza en ciertas ecuaciones, posiblemente debido a su forma, simetría o estética general.
Aunque para un psicólogo el resultado puede parecer sorprendente, para los que se mueven en un universo de ecuaciones el resultado es obvio, pues experimentan placer todos los días al apreciar la belleza de determinadas construcciones matemáticas. Para estos individuos la lectura de la demostración elegante de un teorema produce sensaciones muy parecidas a la de escuchar una melodía.
Desde Platón se ha discutido mucho sobre el concepto de belleza. Obviamente este concepto es muy complicado y quizás sea imposible capturarlo a través de un sistema de resonancia magnética nuclear funcional. Este tipo de estudios al fin y al cabo, como algún crítico ha mencionado, sólo miden el juego entre la recompensa, la toma de decisiones y la respuesta emocional. Pero nada dicen de lo que es la belleza.
Zeki admite que la belleza no está perfectamente definida, pero que su estudio podría desembocar en una comprensión más profunda de la idea y que el estudio, al fin y al cabo, revela qué mecanicismos neuronales permiten experimentar la belleza. “El asunto central que emerge de este trabajo para el futuro es por qué una ecuación es bella.”
Este estudio encuentra, por ejemplo, que la belleza de las ecuaciones no es enteramente subjetiva. La mayoría de los matemáticos están de acuerdo que la identidad de Euler (ver ecuación de cabecera) posee una gran belleza. En esa identidad están relacionados los números más significativos de las Matemáticas. Pero la más fea de las ecuaciones usadas en el estudio es esta de Ramanujan para el inverso de π:
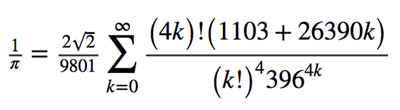
|
Al parecer, y según dice alguno, si se la mira no se aprende nada sobre $pi;. Es una ecuación que no tiene gracia y los números que usa, como 9801, parece que podrían ser sustituidos por cualquier otra cosa.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=4363
Fuentes y referencias:
Noticia en Cientific American
Artículo original.
12 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





miércoles 12 marzo, 2014 @ 8:07 pm
Estoy seguro de que si llegásemos a contactar con una civilización avanzada, de esas típicas de la Sci-Fi, toda de Yodas sobrados de la vida que están de vuelta de mil y un Bibáns, nos mirarían desde el hombro (o su equivalente cultural) y nos dirían, «sólo unos simples como vosotros no saben apreciar la belleza del inverso de Pi de Ramanujan».
El detalle es que las emociones parecen claramente imprescindibles para poder apreciar la belleza.
jueves 13 marzo, 2014 @ 8:23 am
No concibo sentir la belleza o la fealdad sin emoción. Creo que percibidas una u otra la respuesta inmediata es el sentimiento emotivo.
A la percepción de la visión le sigue la formación de la imagen, aunque sé que se da la «visión ciega». En paralelo sólo cabría captar una perfección -o algo así- sin emoción, pero perfección no es necesariamente belleza y viceversa.
jueves 13 marzo, 2014 @ 8:33 am
Pienso yo -y sólo es un pensar- que todas estas maravillas, como esa ecuación que parece unir mundos ajenos en una breve expresión, son consecuencia de sólo unas pocas premisas compatibles, así que, por ello, las matemáticas son universales y pueden describir tan exactamente la naturaleza; o eso nos parece, puesto que juzgamos dentro de ellas. Es como estar dentro de un universo: todo lo veremos según el contenido, conocido o no, de ese universo. Como digo, es solo un pensar.
jueves 13 marzo, 2014 @ 7:15 pm
Sin emociones no sólo no podríamos apreciar la belleza de la ecuaciones sino que tampoco podríamos retenerlas en la memoria de modo firme.
La parte del cerebro que se encarga de las emociones (sistema límbico) desempeña también un papel fundamental en la consolidación de la memoria: recordamos mejor aquello que nos ha causado una emoción intensa. En este sentido sería cierto que es bueno aprender divirtiéndose, pero no menos cierto que «la letra, con sangre entra». En el caso que nos ocupa nos será más fácil recordar la identidad de Euler por su belleza y sencillez, pero también es muy posible que no olvidemos el 9801 de la de Ramunujan por ser feo e inusual.
El cerebro se ve atraído por formas geométricas sencillas y simétricas como círculos, esferas o cuadrados.
He leído el artículo original y veo cierto patrón ya que entre las ecuaciones valoradas como más bellas está también la identidad (trigonométrica) de Pitágoras y las ecuaciones de Cauchy-Riemann, que tienen en común el ser muy sencillas.
Entre las peor valoradas, aparte de la de Ramanujan, citan la ecuación funcional de Riemann de la función zeta, que es bastante más larga y maneja valores complejos.
Es una lástima que no hayan puesto un listado de todas las fórmulas que han utilizado, ya que me quedo con la duda de si había alguna de Einstein, de cuyas f´romulas siempre he oído decir a los físicos que encierran gran belleza.
viernes 14 marzo, 2014 @ 8:19 pm
No creo que el concepto de belleza de una ecuación sea algo aprendido.Cuando entiendes todo lo que te dice una ecuación es imposible no sentirse emocionado. Y sé creo que hay ecuaciones más bellas que otras, por ejemplo esa identidad de Euler que aparece ahí arriba, es de una belleza tremenda. Y luego está la íntima satisfacción (emoción) que te produce la resolución de un problema matemático. Hay ecuaciones extraordinarias, como la conocida F=ma, ¿ y qué decir de la ecuación de Dirac para el electrón que combina la relatividad general con la mecánica cuántica, una especie de puente entre lo discreto y lo continuo?.O la belleza de las ecuaciones de Shannon sobre la cantidad de información contenida en un mensaje, que es de una sencillez magnífica y sobre la calidad de un medio de transimisión.
– Lo mismo diría sobre la música clásica (no es concepto de belleza aprendido).Muchas personas que no tienen una formación musical clásica, aprecian la gran música y siente una emoción real al escuchar las grandes composiciones.
sábado 15 marzo, 2014 @ 9:52 am
Hombre, «lluís», no puede ser que la percepción de esa belleza sea independiente de lo aprendido. Eso no viene de serie aunque, como todo, ha de tener su base genética. Pero quien no sepa lo que significa «e», «i» o «pi», ya me contarás lo que va a sentir. Por otra parte sabes que la alergia a las mates es tan general que cualquier editor pondrá muchas pegas para lanzar un libro con fórmulas.
No puedes compararlo con la música. Como mucho, con una partitura que, a los que no la sabemos leer, no nos dice nada.
Abrazos matemáticos y musicales.
sábado 15 marzo, 2014 @ 12:17 pm
Hombre, tomás, ¿dónde se aprende la belleza de un arco-iris?,¿dónde se aprende la belleza de una puesta de sol?, dónde se aprende la belleza de una tormenta de rayos y truenos?..bueno es posible ( o muy probable) que quien no sepa lo que significa «e» «i» o «pi», o el número de Liouville,por ejemplo,no sienta nada ante una fórmula o un número matemático remarcable, pero puede que sienta otra emoción, desprecio por ser incapaz de entender eso o bien otra emoción, curiosidad por tratar de entender el significado.Hay emociones tanto en sentido positivo como en sentido negativo,al menos tal como lo veo yo.
Eso,siempre tomás, abrazos matemáticos y musicales.
domingo 16 marzo, 2014 @ 8:35 pm
A ver, mi buen amigo, es posible que, simplemente, tal cosa o tal otra no le diga nada a nuestro sujeto, porque no pertenezca a su «mundo circundante». Por ejemplo si yo veo en medio de la calle una pila de libros, seguramente me acercaré e inclinaré la cabeza por ver algún título, e incluso me atreveré a coger uno de ellos para saber si es de mi interés. Pero un perrillo que por allí pase entenderá que es un buen mojón para marcar su territorio y los mojará sin remedio.
Eso del mundo circundante nos puede ser muy útil en este intercambio de opiniones.
Un fuerte abrazo.
martes 18 marzo, 2014 @ 6:38 pm
Queridos «lluís» y «tomás»:
¡Ja, ja!, es curioso lo de los perros, el nuestro es un auténtico «marcador» que puede levantar la pata más de 20 veces en un sólo paseo de 15 minutos. Y le pone mucho interés, aunque a veces le falla el sentido común y marca un pequeño pelotón de ramas secas de esos que se va a llevar el viento en cuanto sople la menor brizna.
En cuanto a la belleza y si es aprendida o no, podemos tomar el ejemplo del estudio que nos ocupa, en el que las ecuaciones han sido valoradas por un grupo de profanos y por otro de entendidos: la impresión inicial (que tiene un enorme peso específico para el cerebro) seguramente sea común en ambos grupos, el cerebro emite un juicio rápido (como siempre artístico e intuitivo) en el que considera aspectos como la sencillez de la fórmula o si tiene cierta simetría. Para los que entienden de matemáticas se añaden más tarde otras connotaciones como podrían ser la utilidad o repercusión de la fórmula, etc…pero nuevamente tendrán un gran peso aspectos de índole artística y muy subjetivos. Así, es posible que no me guste una ecuación porque no me cae bien el autor de la misma, o porque cometí un fallo con esa ecuación en un examen.
sábado 22 marzo, 2014 @ 10:14 am
Mi querido amigo «lluís» me ha hecho trampa. En su 5 defiende claramente y con feliz entusiasmo la belleza de algunas fórmulas que ha de ser reconocida universalmente incluso por los más negados en mates y luego, en su 7, ya admite ciertas emociones incluso negativas. Y eso no vale a no ser que se confiese.
Así que me he decidido y he hecho una consulta a la que considero un verdadero paradigma. Mi querida hermana se reconoce catastrófica tanto en mates como en geometría, lo que no obsta para que haya triunfado en su profesión como profesora de lengua con algún reconocimiento oficial a su labor. Quiero decir con esto que inteligencia no le falta. Pero quizá a causa -digo yo- de no haber tenido ningún buen profesor, repito que, en esas disciplinas, es fatal.
Teníamos como unos doce años cuando quiso que le explicase -creo recordar- la fórmula del área del triángulo. Aquello era lo mío, así que, seguro de mí, me dispuse a ello. Nada más empezar me para y me dice que aquello no era así porque la hermana y monja ¿Filomena? lo explicaba de otra manera. Yo le dije que cualquier cosa puede demostrarse de varias formas y que bastaba con que fuesen correctas, no tenían por qué ser iguales. Pero no hubo forma y aquello significó el divorcio matemático-geométrico entre ella y yo. La tal ¿Filomena? triunfó sin necesidad de estar presente. Pues bien, estos días ha venido a ver a mi padre, que acelera hacia los 101, y he aprovechado para contarle mi pequeña disputa con «lluís» y, a la vista de la ecuación del artículo, me diera su opinión.
No le dice nada, pero nada de nada. Y al enseñarle otra algo más compleja puede escapar corriendo. Para ella es un mundo al que niega existencia. He de decir algo que suele ser de común aquiescencia: le encanta, pero también le ha sido negada la posibilidad de aprender música: tiene oreja, pero no oído, aunque ciertamente la disfruta, lo que me parece asombroso porque según me confiesa hubo de aprenderse un truco memorístico -en eso es fenomenal- para distinguir las notas musicales. No es capaz de diferenciarlas. ¿Cómo aunar eso con su éxito en enseñanza a hipoacúsicos en lo que fue pionera? Quizá resulta compatible un lóbulo parietal débil con un temporal extraño, fuerte en memoria y flaco en audición y un hipocampo supereficaz además de las áreas de Broca y Wernicke, pero con la tan próxima área auditiva muy ineficaz. No creas, amigo Miguel Ángel, que me tomo el cerebro como algo tan compartimentado como puede parecer en mi comentario. Pero sí que cualquier mente resulta asombrosa.
Sin duda el cerebro lo es.
También quiero decirte algo, amigo «lluís» y es que afirmé que una partitura no me decía nada y no es cierto, porque soy aficionado a la pintura y me encantan tanto los escritos en chino, japonés o árabe -incluso la cuneiforme- como esas partituras. Tienen algo armonioso que no puedo encontrar en nuestra escritura actual, ni siquiera manuscrita. Y no caigo en el por qué.
Abrazos para ambos.
miércoles 26 marzo, 2014 @ 1:53 pm
Tomás, el rongorongo te tiene que encantar:
http://upload.wikimedia.org/wikipedia/commons/0/02/Rongorongo_ligatures.png
O el lineal B (que es un silabario de la lengua… ¡griega!):
http://www.unicode.org/charts/PDF/U10080.pdf
La historia del desciframiento del lineal B también es de una enorme belleza en sí misma.
O el alfabeto latino original, que se escribía en bustrófedon (algo muy democrático para un zurdo) o en espiral, partiendo de un punto central y dando vueltas xD.
jueves 27 marzo, 2014 @ 11:34 am
¡Caramba! El rongorongo me recuerda una especie de danza, como si en las figuras hubiese una vibración armoniosa. El sitio donde me has enviado para el «lineal B» no me decía nada, pero he mirado en Wikipedia y también me sugiere movimiento, en especial la tablilla del «vendedor de aceite».
Abundando en este tipo de cosas creo que la inteligencia humana debió asentarse en relacionar lo aparentemente inconexo. ¿Qué piensas de ello?
Saludos y gracias por los envíos.