NeoFronteras

Un estudiante de 20 años gana el premio de 25.000 dólares de un concurso convocado por Stephen Wolfram para quien demostrase la capacidad de cómputo universal de la máquina de Turing 2,3.

Una posible evolución de una máquina de Turing 2,3 se muestra de izquierda a derecha, estando la cinta representada verticalmente. Foto: wolframscience.

Usted, que está sentado delante de un ordenador o computadora, quizás no sea consciente de la teoría matemática que fue necesario desarrollar en las primeras décadas del siglo pasado para poder crear este tipo de máquinas.
Hubo muchos científicos (físicos y matemáticos principalmente) implicados en este campo. Uno de ellos fue Alan Turing, que en los años treinta desarrolló la máquina conceptual de cómputo que lleva su nombre. Pudo demostrar sobre el papel que se puede crear una máquina de Turing capaz de emular cualquier otra máquina de Turing.
Nuestros ordenadores y computadoras están basados en última instancia en este tipo modelos computacionales. Hay varios de ellos, como el cálculo lambda y otros, pero suelen ser equivalentes a la máquina de Turing y ésta es probablemente el modelo computacional más paradigmático y famoso.
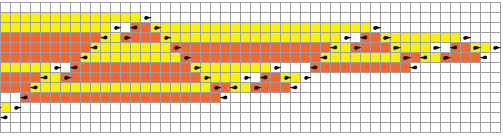
La máquina de Turing es muy sencilla y se basa de una cinta sobre la que se escribe información mediante una cabeza lectora y grabadora que puede adoptar distintos estados. La cabeza lectora se basa en un conjunto de reglas fijas para moverse, leer y escribir caracteres sobre la cinta. El número de caracteres distintos que puede escribir o «colores» se fija al inicio, al igual que el número de estados que la cabeza lectora puede adoptar. Estos dos parámetros determinan la complejidad de la máquina, de este modo una máquina de Turing 10,8 puede adoptar 10 estados y usar 8 colores. Cuantos más estados y colores use más compleja será la máquina de Turing en cuestión.
En los años cincuenta y sesenta los científicos se plantearon cuál se sería la máquina de Turing más sencilla con capacidad de cómputo universal. Es decir, capaz de emular cualquier cálculo computable. A principio de los sesenta Marvin Minsky pudo demostrar que una máquina de Turing 7,4 tenía la capacidad de cómputo universal.
En los ochenta Stephen Wolfram, matemático famoso por crear el programa Mathematica, estudió los autómatas celulares, que en algunos casos eran equivalentes a máquinas de Turing, sospechando que muchos de ellos tenían la capacidad de cómputo universal. Lo demostró para el autómata con la regla 101 y encontró además que la Turing 2,5 era universal.
Una de las consecuencias que se podían extraer de estos resultados era que la computación universal era particularmente ubicua, que debía de darse en muchos sistemas y por tanto que se debía de encontrar en la naturaleza. Según Wolfram todo esto estaría conectado con cuestiones fundamentales en la ciencia, la naturaleza, la matemática y las ciencias de la computación. Además podría explicar cómo a partir de reglas muy sencillas surge la complejidad en los sistemas.
Más tarde demostró que la Turing 2,5 es universal y sospechó que la Turing 3,2 era demasiado simple para ser universal. Además, se sabe que las más sencillas, como la Turing 1,2, no son universales.
Para poder rellenar el hueco Wolfram lanzó un reto dotado con un premio de 25.000 dólares para aquel que fuera capaz de demostrar que la Turing 2,3 era universal.
Ahora el estudiante de electrónica y computación de 20 años Alex Smith de la Universidad de Birmingham (RU) ha ganado el premio al ser capaz de demostrar que, efectivamente, la máquina de Turing 2,3 es universal. Se ha basado en otro modelo computacional denominado sistema de etiquetas (tag system) que se sabe es universal, demostrando su equivalencia con la Turing 2,3. La demostración completa ocupa 44 páginas.
El resultado no es particularmente relevante en ciencias de la computación y a la mayoría de los expertos les trae sin cuidado por considerarlo pasado de moda, pero puede estimular nuevos trabajos en el área. Además nunca es tarde para un resultado teórico bonito.
Smith, por otro lado, dice no tener grandes proyectos para el dinero del premio, y de momento lo va simplemente a ingresarlo en el banco.

Fuentes y referencias:
Anuncio del premio.
Galería.
Demostración en pdf.
Introducción al problema.