Universo, simulaciones y computación
Un par de resultados recientes hablan de la relación entre el Universo y la computación.
|
La ciencia ficción ha propuesto reiteradas veces que podría ser posible que fuéramos una simulación en un ordenador. Esta idea ya se había propuesto antes de que se estrenara Matrix, que obviamente bebe de las fuentes de Philip K. Dick.
Según esta idea todo los que nos rodea nos rodea: la Tierra, el Sistema Solar, la Vía Láctea y todo el Universo, no sería más que una simulación en un computador que algo parecido a unos dioses tendrían en algún lado. Toda la historia de la humanidad, sus logros o sus obras serían el subproducto de una gran simulación computacional. Nuestros sentimientos, pasiones, mezquindades, buenas obras y los hallazgos de la ciencia también serían unas cadenas de bits en frenética combinación entre sí. Todo el Universo duraría hasta que alguien al otro lado apretara el botón de reset y entonces toda nuestra existencia caería por completo en el más absoluto olvido.
Pero una cosa es lo que dice la ciencia ficción y otra lo que dice la ciencia. La realidad es que nosotros no podemos simular más que una pequeña parte del Universo en nuestros computadores. Simular todo el Universo se antoja imposible. Quizás podremos algún día simular un universo alternativo menos ambicioso, pero no el nuestro. No tenemos suficientes átomos en el Universo para simular la autoorganización de todos los átomos del propio Universo. Si nos vamos a la escala de lo muy pequeño ni siquiera podemos simular la estructura del propio espacio-tiempo, pues incluso carecemos de una teoría para ello. A lo más podemos hacer algunas simulaciones en el retículo de la Cromodinámica Cuántica, que nos proporciona predicciones de cómo se organizar los quarks entre sí. Y estas simulaciones sólo llegan el femtometro de tamaño.
Hace unas semanas hubo cierto revuelo en la blogosfera sobre un artículo publicado en los ArXiv por parte de Silas Beane, de la Universidad de Bonn (Alemania), y sus colaboradores. Según estos teóricos se podían encontrar pruebas de que el Universo es una simulación, aunque tampoco aseguraban que así fuera.
Un problema que surge con esta idea de la simulación es que las leyes de la Física parecen vivir en un continuo en lugar de en un espacio discreto. Si fuéramos una simulación tendrían que ser lo segundo, tendríamos que ver los “píxeles” o los “bits” que componen la “realidad” a algún nivel.
Beane imaginó que si a cierto nivel hay una discretización entonces debe de tener un efecto en lo que observamos en el Universo, sobre todo en los procesos muy energéticos. Si nos fijamos un poco es similar a la idea, menos esotérica, de ver la estructura del espacio-tiempo a la escala de Planck usando fotones gamma y midiendo diferencias en su tiempo de vuelo a lo largo de grandes distancias. En este caso el efecto se debería a que ninguna partícula o efecto puede ser menor que la celda unidad de la simulación.
Estos investigadores especularon que si el Universo es una simulación entonces debe de haber un corte en el espectro de energía de las partículas de alta energía. Ese límite existe y se llama Greisen–Zatsepin–Kuzmin (GZK), pero es atribuido a la interacción de los rayos cósmicos ultraenergéticos con los fotones del fondo cósmico de microondas, de tal modo que, en su viaje por el Universo, las partículas de rayos cósmicos más energéticas van perdiendo energía y al medir su energía nunca encontramos que superen el límite GZK.
Pero estos investigadores asumieron que si el Universo es una simulación y el retículo de simulación está compuesto por celdas cúbicas entonces habrá una anisotropía en este efecto. No sería lo mismo que una partícula viajase en la simulación en dirección a las caras de cada cubo que en dirección hacia las esquinas. Esto afectaría a los rayos cósmicos que medimos, pues tendrían una dirección de propagación preferente a través de las caras de los cubos. Esto podría ser medido.
Sin embargo, la idea presenta un par de problemas. Uno es que los semidioses que nos simulan pueden haber elegido un retículo distinto al cúbico, quizás hexagonal o triangular. El otro problema es que si la idea es cierta y el límite GZK corresponde a este fenómeno, entonces el tamaño de cada celda del retículo es increíblemente pequeño, en concreto de 10-27 metros.
Obviamente este tipo de cosas no se plantean seriamente (pese a lo que dicen los autores en su artículo) y son más bien un divertimento de físicos teóricos, aunque sirven para pensar sobre problemas fundamentales. Y, como los filósofos ya solucionaron en el pasado, si somos una simulación y ésta es tan buena que es indistinguible de la “realidad” entonces no importa y la simulación es tan “real” como deseemos que sea.
Pero si no somos una simulación quizás podamos creer en algo menos drástico. Quizás el Universo en sí mismo es un gran computador. Según esta visión, dado un estado inicial determinado como input, el Universo genera estados futuros como outputs de una simulación. Esta idea se ha propagado por ciertos ámbitos sin que se haya considerado su validez o se hayan tenido en cuenta otras alternativas. Es meramente una asunción que uno debería cuestionar.
Ahora Ken Wharton, de San Jose State University (California), ha escrito un artículo en el que desafía esta idea. Según él esta hipótesis es muy antropocéntrica y asume que el Universo funciona de la misma manera que los humanos resolvemos problemas en la Física.
Entre los problemas que Wharton ve a esta idea está el que para computar el mundo físico primero hay que hacer una correspondencia entre su estado y un estado matemático que es el que se va a computar. Luego ese estado matemático evoluciona hacia otro estado y este nuevo estado se pone en correspondencia con el mundo físico. Pero esto no está permitido por la Mecánica Cuántica a no ser que asumamos que el estado final es probabilístico. Ni siquiera el Universo conoce que estado particular va a adoptar. Además, cuando el Universo es medido se produce un output específico por el mismo acto de medición y un computador clásico no puede tener en cuenta esto.
Quizás lo más interesante de este pensamiento es que las leyes que gobiernan el Universo no pueden expresarse en términos computacionales.
Wharton propone una hipótesis alternativa basada en la idea de Lagrange según la cual las leyes físicas están basadas en el principio de mínima acción.
Así por ejemplo cuando una haz de luz se refracta la pasar del aire al agua, no lo hace por algún tipo de algoritmo, sino porque es el modo más eficiente de propagarse. La trayectoria entre el punto inicial y final unidos por ese haz de luz sería la distancia más corta entre esos dos puntos de entre todas las posibles.
Lo malo es que puede que el Universo tampoco funcione bajo el principio de mínima acción, pues éste no es más que un buen truco que hemos encontrado para resolver ciertos problemas en Física. Además de ser una idea ingenua con la que trabajar.
De todos modos, la idea básica de Wharton de desafiar la hipótesis del Universo como un computador es buena y, sobre todo, esperemos que dé pie a otras alternativas mejores. Al fin y al cabo, es así como funciona la ciencia, sobre todo si esas nuevas ideas se pueden contrastar con la realidad de algún modo.
Yace un problema epistemológico en esa dicotomía entre modelos de realidad y realidad, entre simulaciones de realidad y la realidad, entre lo que sabemos sobre la realidad y la realidad misma, entre una mente perteneciente a la realidad pensando sobre la realidad a la que pertenece o entre un computador físico simulando una parte de la realidad a la que él mismo pertenece. Por no saber no sabemos la relación real entre Matemáticas y realidad, ¿son éstas simplemente una herramienta o tienen alguna correspondencia con la propia realidad? Ya sólo nos quedaría sacar a colación a Gödel y Turing.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=3982
Fuentes y referencias:
Artículo en ArXiv.
Artículo en ArXiv.
36 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





lunes 10 diciembre, 2012 @ 8:06 am
Yo lo tengo claro: Para mí las matemáticas son un lenguaje extremadamente preciso para describir la realidad; mucho más que el lenguaje vulgar, pero sólo un lenguaje; o múltiples lenguajes, según lo que precisemos describir. Y su utilidad es proporcionar deducción a la inducción del método científico.
Lo que sucede es que eso sólo puede ser calificado como un principio, no como algo que pueda demostrarse. Pero también la validez del método científico es algo así como un principio; por no llamarles a ambos ¿fe?…
lunes 10 diciembre, 2012 @ 5:22 pm
si, las matematicas existen si eso quieren escuchar, pero existen de la misma manera que existen las palabras que ahora escribo,por necesidad, en el mundo de las ideas, con la salvedad que las matematicas pueden describir no solo este universo sino todo universo posible e imposible.Un ejemplo mas practico ¿de donde surgen las probabilidades? ¿que hace que cierta partícula que individualmente no presente mas propiedades que las básicas a medida que adquiere mas cantidades vaya tomando forma de una distribución adquiriendo propiedades que lo ligan al sistema del que forma parte? yo citaria a norther tambien, la simetria necesita conservacion. Muy pragmático casi ontologico el ultimo párrafo.
lunes 10 diciembre, 2012 @ 8:29 pm
El asunto de las Matemáticas nos puede remitir incluso a Platón, pues se puede pensar que transcienden al ser humano.
Son un producto cultural, pero no tienen origen cultura. Si así fuera dos civilizaciones distintas no llegarían a los mismos resultados, cosa que sí lo hacen aunque usen notaciones distintas (esto sí es cultural).
Podemos asumir que otras civilizaciones en galaxias remotas llegan a los mismos resultados matemáticos. ¿Llegarían otros entes en otro universo a los mismos resultados aunque sus leyes físicas sean distintas?
martes 11 diciembre, 2012 @ 9:14 am
«… pero no tienen origen cultural». Toda cultura tiene un origen biológico más o menos lejano. Y toda matemática comienza por 1 + 1 = 2. Muchos animales pueden ir bastante más lejos. Creo que los cuervos llegan hasta ocho.
Dos civilizaciones algo distintas, por lo menos hace algunos siglos, dirán: arbre, tree, árbol, y todas se refieren a lo mismo. Y es que coincidimos en que bajamos de ellos. Bueno, es un juego de ideas, pero no estamos tan lejos de esas tribus -no sé si ya extintas y creo que australianas- que sólo sabían contar hasta 3 y más allá era «mucho» o «muchos» y cuya expresión era cogerse los cabellos. Yo, sería ignorante por calvo.
martes 11 diciembre, 2012 @ 5:29 pm
Hola, amigos. Aunque soy lector habitual de neofronteras, no suelo comentar; mas no he podido evitar la tentación de participar, viendo la cantidad de problemas tan interesantes que aquí se plantean y que se relacionan con aquello a lo que me dedico (filosofía). El problema de las matemáticas me parece una de las grandes cuestiones ontológicas que competen tanto a la filosofía como a la ciencia. Parece ser, por lo menos dentro del ámbito de la filosofía, que la existencia de las matemáticas llevan consigo la necesaria adopción de un realismo metafísico; esto es, la existencia de entidades cuya «verdad» no depende del mundo (2+2=4 nunca dejará de ser verdad pase lo que pase en el mundo) implica, de algún modo, que hay realidades que subsisten más allá de toda intervención del sujeto de conocimiento (aunque la dicotomía sujeto-objeto también es cuestionable). Aunque es cierto que todos pensamos en las matemáticas, como dice Tomás, son una herramienta que, junto a la lógica, nos permite formalizar teorías y dar cuenta de fenómenos empíricos. Sin embargo, el problema de su estatuto ontológico sigue ahí, sin resolverse; y como dice Neo, podemos remontarnos a Platón y los griegos para ver que estas cuestiones estaban allí ya. Obviamente son indemostrables, y ahí entramos en el famoso trilema de Münchhasen y la «autocontradicción performativa» de Apel.
En cuanto al problema de cómo saber si estamos o no en una simulación (¿somos un cerebro en una probeta?), siempre podríamos argumentar sobre las condiciones de posibilidad de lo que ello implica (al igual que el famoso enunciado del «principio antrópico»). No sé, veo muchos interrogantes y no quisiera extenderme más. Para terminar, una pregunta a Neo: ¿los átomos se pueden autoorganizar? Lo digo porque tenía entendido que, dentro del pensamiento complejo (niveles de organización), la autoorganización era exclusiva de los sistemas vivos, no físicos. Aunque no lo tengo claro.
Un saludo a todos!
miércoles 12 diciembre, 2012 @ 9:37 am
Todo depende a lo que se llame autoorganización. Un sistema vivo está hecho de átomos, así que los átomos se pueden autoorganizar. Hay determinados proceso no biológicos que se autorregulan, así que de algún modo se autoorganizan.
Lo que está claro es que para que surjan proceso complejos se deben dar propiedades emergentes, así que el todo no es la suma de las partes. Tampoco los átomos lo son todo, hay leyes físicas, preparaciones, aislabilidad… Entidades que también tienen un papel.
miércoles 12 diciembre, 2012 @ 9:52 am
Estimado «danielperes»:
Estoy seguro de que Neo te contestaría o te contestará infinitamente mejor que yo. Y seguramente con más fundamentados principios. Lo que pasa es que soy un discutidor nato y no puedo evitar ser un metomeentodo. Además «por alusiones».
Durante mucho tiempo no hubo átomos tras el Big Bang. Y no había ningún organizador. Supongo que las condiciones ambientales los llevaron a construirse primero como hidrógeno. Por tanto, si repetimos esas condiciones, los átomos se formarán.
Dices: «… sistemas vivos, no físicos». Que yo sepa los sistemas vivos son sistemas físicos -y sólo físicos para mi, claro, que no tengo alma y soy tan materialista-.
En cuanto a que 1+1=2, fíjate que yo lo refiero a las matemáticas. Tu 2+2=4 es absoluto («… nunca dejará de ser verdad…). Y no señor, no es cierto. Incluso mi afirmación habría de haberla referido al sistema más vulgar y conocido: la aritmética elemental. Porque primero hay que enunciar las reglas por las que regirnos y, en esa aritmética elemental, al + le asignamos que, tomando el primero y aplicándole el operador +, al añadirle otro me da sel siguiente. Quizá debería haber empezado por decir que 1 es un número natural o que pertenece al conjunto de los números naturales. Bueno, pues resulta que ese número siguiente obtenido, siempre pertenecerá a los números naturales. Piensa que ese mismo operador puede indicar otro tipo de operación; por ejemplo (2H2 + O2 = 2H2O + energía) que, como ves, es bien distinta. Ya sé que todo esto lo sabes pero sucede que, a veces, no pensamos en ello. Entonces, las diferentes matemáticas, quiero decir aquellas que utilizan otro tipo de signos, se ocupan de diferentes ámbitos y son útiles -para evitar a Godel- en ellos y sólo en ellos. Voy a ponerte un ejemplo muy tonto, pero es que tampoco doy para mucho más y a los filósofos hay que trataros con mucha delicadeza: 2 manzanas + 2 peras no se pueden sumar, pero 2 frutas(manzanas) + 2 frutas (peras) = 4 frutas (peras y manzanas) y es verdad. Bueno, espero que me perdones por ponerte esos ejemplos tan triviales. Pero esto lo digo por tu afirmación de que «2+2=4 nunca dejará de ser verdad pase lo que pase en el mundo». Porque tampoco es cierto. Eso sucederá sólo dentro de un sistema que hemos convenido. Por ejemplo yo afirmo con tanta razón como tú que 2+2=11 en un sistema de base tres, en vez del de base diez que estamos acostumbrados a utilizar.
Y dejo, si quiere, paso a Neo con la ilusión de que no me corrija mucho y que, como tú, excuse mis errores.
Cordiales saludos y verdades relativas.
miércoles 12 diciembre, 2012 @ 10:00 am
¡Vaya! Neo ha sido más rápido que yo y, aunque he empezado antes, se me ha colado. Como ves, la sabiduría se acompaña de la brevedad y la velocidad. Cuanto dice lo suscribo humildemente.
Saludos para ambos.
miércoles 12 diciembre, 2012 @ 10:15 am
Me ha gustado lo de «propiedades emergentes» neocitadas. Y es que, -no, evidentemente, por Neo que sabe perfectamente lo que dice, ni por el caso, que le viene al pelo- sino porque muchas veces se utiliza gratuitamente.
Porque una propiedad emergente, se da cuando no surge de las solas propiedades conocidas de las partes. Es decir que hay variables desconocidas que no tenemos en cuenta y que surgen precisamente al darse el proceso emergente. En cierto modo un paso de más largo alcance, y mucho más profundo que mi pueril explicación sobre el signo +.
Pues eso, que podía haberme callado.
Abrazos.
miércoles 12 diciembre, 2012 @ 11:18 am
Muy interesantes todos los comentarios. Mi punto de vista es más «utilitario» por lo que estoy de acuerdo en que las Matemáticas, como cualquier otro tipo de pensamiento es una herramienta cuyo objetivo último es incrementar nuestras posibilidades de supervivencia en términos darwinianos al igual que lo son el resto de «acciones» que realizan los seres vivos, con independecia de que el «bicho» que las realiza sea consciente (como los seres humanos) o inconsciente (si entendemos por tal animales «inferiores» o plantas)tanto de la propia «acción» como del objetivo último de la misma. Asimismo creo que puesto que para sobrevivir hay que hacer muchas «acciones» diferentes entre sí, cada una de ellas requiere de herramientas especializadas. En este sentido las matemáticas serían la herramienta más sofisticada que utilizamos los humanos para hacernos un modelo de algunos aspectos concretos del mundo (que sospecho que compartimos con la mayoría especies, al menos en su forma más elemental de aritmética básica de «poco» es menos que «mucho»): por ejemplo para optar entre subirnos a comer a un árbol con mucha fruta o a un árbol con poca, humanos y simios utilizamos básicamente las mismas matemáticas y el que hierre en sus «cálculos» (incluído el riesgo de perder demasiado tiempo en el calculo) será penalizado en su supervivencia. Si esto lo ampliamos a sociedades humanas en las que se genera propiamente el conjunto del conocimientos culturales que llamamos «Matemáticas» vemos que las sociedades más avanzadas (en el sentido de con mayor éxito en términos de supervivencia)son las que han desarrollado la herramienta «de las matemáticas» a su máximo nivel.
miércoles 12 diciembre, 2012 @ 6:51 pm
Las matemáticas son un lenguaje universal (por ejemplo, el teorema de Pitágoras se cumple aquí y en el otro extremo del Universo), y por tanto tienen mucho que ver con la realidad.Si es que realmente no son la propia realidad (en ello estarían de acuerdo tanto Pitágoras como Penrose).
-El principio de «mínima acción» (algunos de cuyos efectos comprobabables lo son los espejismos)no es otra cosa que el principio de tiempo mínimo de Fermat y conduce por tanto a los fenómenos de reflexión y refracción de la luz (Ley de Snell), así que ese principio parece funcionar en el Universo.
– También cabe considerar que Boltzmann caracterizó la entropía como el número de estados microscópicos distintos en los que se pueden hallar las partículas que componen un pedazo de materia de tal forma que siga pareciendo el mismo pedazo desde un punto de vista macroscópico.Algo parecido a la entropía de Boltzmann, hizo el matemático Claude Shannon (injustamente un tanto olvidado)al buscar el modo de cuantificar la información contenida en un mesaje.Con ello dió con una fórmula que matemáticamente tenia el mismo aspecto que la de Boltzman, asi que las entropías de Boltzmann y Shannosnson equivalentes matemáticamente consideradas.Por todo esto Shannon probó que la Teoría de la Información es algo tan fundamental, para abordar el problema de la realidad,(el Universo) como lo pueda ser la teoría de partículas elementales (que al fin y al cabo se rige por las mismas leyes que las de la información.
Y luego cabe pensar en el principio de Heisenberg y el problema de la medida.
Quizás el Universo no sea computacional, pero si esos estados matemáticos evolutivos que propone Wharton pueden ser puestos en correspondencia con el mundo físico y se asume que la MC es probabilística parece lógico pensar que «ni siquiera el Universo conozca el estado que va a terminar adoptando».Y si bien un computador clásico no puede tener en cuenta todo eso. quizás podría hacerlo un computador cuántico.
jueves 13 diciembre, 2012 @ 12:44 am
Muy buenas a todos.
No debes preocuparte Tomás, me encanta discutir y me aburriría mucho si no tuviésemos visiones diferentes. En relación a la cuestión de la autoorganización, me refería a la obra de Edgar Morin, la cual me tocó estudiar duramente en una asignatura de la carrera. El caso es que Morin, al cual tuve oportunidad de conocer en persona, distingue tres grandes sistemas o niveles de organización: físico, biológico y socio-cultural. Obviamente este pensamiento «complejo» es emergentista, y las propiedades del sistema nunca son reducibles al comportamiento de las partes constituyentes (lo cual va en contra del tan repetido principio de economía de Occam). Es obvio, Neo, que los sistemas vivos están hechos de átomos, pero también es cierto que aparecen cualidades emergentes no reductibles al nivel físico, y que suponen un nuevo nivel organizativo. Según dijo el propio Morin (que tampoco debe tomarse aquí como algo irrebatible) los sistemas físicos no son abiertos, es decir, no se «alimentan» del exterior. La idea para diferenciar sistemas físicos y vivos la tomó de Prigogine y su concepto de «estructura disipativa». De ahí que diga que el sistema vivo es «autónomo» respecto del ecosistema (o socioecosistema en nuestro caso), pues éste puede emplear la energía del exterior para autoorganizarse lejos de las condiciones del equilibrio. Además arguye razones que tienen que ver con la «computación y «cogitación» celular, algo que difícilmente puede atribuirse a los átomos en un sistema que se autorregula (como las celdas de Benard). Pero bueno, en realidad nunca he estado seguro de casi nada, así que tampoco quisiera imponer ninguna verdad a nadie ni nada por el estilo.
En cuanto a toda la entrada de Tomás, tengo tantas cosas que decir (gracias por tu estimulante comentario), pero tampoco quiero abusar de este espacio para hablar más de la cuenta. Tomás, cuando dices «Que yo sepa los sistemas vivos son sistemas físicos -y sólo físicos para mi, claro, que no tengo alma y soy tan materialista» no me refería a cosas u objetos no-físicos, sino a niveles de organización y a toda la parafernalia que se estudia en epistemología, ontología, pensamiento complejo y demás materias. Yo tampoco creo que tenga algo así como un alma, pero esta cuestión supongo que tendremos oportunidad de debatirla más adelante. Y en el tema de las matemáticas, perdóname, porque estaba hablando sin explicitar cosas que tenía en mente, de modo que no me he expresado correctamente. En concreto esa sentencia, la de “2+2=4 nunca dejará de ser verdad pase lo que pase en el mundo”, la he sacado de una clase que tuve de filosofía del lenguaje, donde distinguíamos tipos de enunciados: analíticos a priori y necesarios, y sintéticos a posteriori y contingentes. Las matemáticas siempre han sido vistas como algo a priori y necesario, es decir, el predicado no añade nada al sujeto, de tal manera que su verdad es tautológica. A diferencia de proposiciones sintéticas a posteriori, que son contingentes (a causa de su dependencia del mundo, que nunca fundamenta necesidad, sino tan sólo probabilidad como ya advirtió Hume en su crítica de la inducción). Y por último me gustaría decir algo acerca de lo que dices con la oración «eso sucederá sólo dentro de un sistema que hemos convenido». Parece que el relativismo cultural no es suficiente para dar cuenta de cómo distintas culturas llegan a resultados idénticos en las matemáticas. Y no sé, aunque esté bien alejarse de los dogmatismos, parece que sí que hay verdades absolutas, como que nos entendemos aquí al discutir. Existen ciertas cosas, como el principio de no contradicción, o las condiciones de la acción comunicativa, que no pueden refutarse. El mismo acto de hablar supone aceptar que las palabras tienen cierto significado y que compartimos un suelo común indiscutible. Por eso mismo, al hablar de matemáticas yo veo algo trascendental (no confundir con trascendente), más que un sistema convencional.
Perdonad la extensión de mi comentario. Un saludo muy cordial a Tomás y Neo.
jueves 13 diciembre, 2012 @ 10:40 am
Queridos «lluís» y «danielperes»:
Como la ignorancia da para poco y estoy tratando con una pareja de extraordinarios matemático-filósofos, me voy a remitir a la afirmación de «lluís» (perdona que no incline las letras -ni la cerviz, como debiera-, pero es que no sé cómo hacerlo, pues en mi configuración no tengo barra de herramientas).
Dices, amigo lluís: «… el teorema de Pitágoras se cumple aquí y en el otro extremo del Universo». Y esto enlaza con el sutil «Parece que el relativismo cultural no es suficiente para dar cuenta de cómo distintas culturas llegan a resultados idénticos en las matemáticas» de «danielperes».
Pues eso, para mi, tiene fácil explicación. El teorema de Pitágoras está ahí: es un hecho irrebatible. Aquí tenemos una argumentación que nos lleva a una expresión matemática a2 + b2 = h2. En otra civilización han de tener el mismo hecho que podrán expresar con otras notaciones que no me atrevo a imaginar, pero que querrán decir lo mismo, puesto que están expresando, como repito, un hecho. Así que es una simple traducción. Sirva el -me habréis de perdonar por ser tan elemental- que veamos un árbol y un francés le llama «arbre» pero el alemán espeta: «Baum» -espeta por no decir explota, que estos alemanes son así de firmes (es Bromaun). El árbol es un hecho incontestable y hay múltiples formas de decirlo, todas ciertas. Pero la expresión y su certeza, no son la realidad, son una forma de expresar la realidad.
Para resolver el tema basta pensar: ¿existiría el árbol si el hombre no existiese?: evidentemente sí. Por el contrario: ¿existiría la palabra árbol o cualquier expresión del teorema de Pitágoras -aunque para mí sea tan «hecho» como el árbol material- si el hombre no existiese?: pues no.
Y con esto os dejo, porque pretendía -con evidente fracaso- ser breve.
Abrazos.
jueves 13 diciembre, 2012 @ 10:48 am
Muy interesante el hilo matamaticoemergente ,las emergencias podrían ser muy básicas. Se organizan tres quaks con tamaños de 10 a la -18m y tenemos un protón o un neutrón de 10 a la -15m, solo con que se organicen dos o tres entre unos y otros, ya tenemos un núcleo de 10 a la -14m y si en la organización entra un electrón con un tamaño similar a los quarks, tenemos un átomo con tamaño de 10 a la -10m. Al menos en cuanto al tamaño emergencia parece haber, no quedándome claro que aquí 2+2=4.
Volviendo a la madeja de las simulaciones computacionales, es muy posible que tras finalizar el experimento, al analizar el proceso el «H. sapiens» quede como una pequeño y muy breve conato de emergencia organizativa bastante inestable y desestabilizador, allá por el primer cuarto del experimento. Si no somos un experimento, tenemos todas las papeletas para quedar en le registro fósil como «H. super et autodepredatoris».
Creo que si fuéramos solo una simulación computacional, tendríamos mas posibilidades de que a los superprogarmadores les de por intervenir para cambiarnos algunos paradigmas, que siendo reales, lo pudiéramos hacer nosotros mismos, sabiendo como sabemos, que todas las simulaciones computacionales que somos capaces de hacer nos indican la urgencia de que lo hagamos.
Saludos a todos.
jueves 13 diciembre, 2012 @ 10:58 am
Pues no sé si estoy de acuerdo con»pvl» en eso de que «… las sociedades más avanzadas (en el sentido de con mayor éxito… ) son las que han desarrollado… mateméticas» a su máximo nivel». Pienso en griegos y romanos y en romanos y bárbaros. A mi me parece que yerra; al menos en esa cuestión.
jueves 13 diciembre, 2012 @ 11:04 am
Caramba, Pocosé: Me has dejado con los ojos dando vueltas, o sea, haciendo chirivitas. Ya te leeré más tranquilo.
jueves 13 diciembre, 2012 @ 4:44 pm
Estimado Tomás, de nuevo intervengo, pues has planteado una cantidad de cuestiones filosóficas sumamente interesantes.
Cuando dices «el árbol es un hecho incontestable y hay múltiples formas de decirlo, todas ciertas. Pero la expresión y su certeza, no son la realidad, son una forma de expresar la realidad.» Ahí, concretamente, planteas el debate realismo-idealismo. En este marco, parece que apuntas a que los hechos son construcciones humanas, y, por tanto, defiendes cierto tipo de idealismo (también en relación a las matemáticas). Aunque este debate sigue vivo y no esta resuelto, y aunque también pudiésemos distinguir entre expresión (sintaxis), modelo (semántica) y realidad (ontología) del árbol, voy a ser breve y a esgrimir un argumento a favor del realismo objetivo de los entes matemáticos, en lugar de alargar tanto la discusión.
Frege defiende la objetividad de las matemática porque, según él, se fundamentan en la lógica, cuyas leyes son necesarias y no reductibles a leyes psicológicas. Si tenemos términos singulares que refieren a números naturales (por ejemplo) y que tienen valor de verdad, es porque dichos números existen. Es decir, los componentes singulares de la proposición que refieren a términos naturales son verdaderos o falsos porque los entes matemáticos existen. Como no tenemos referencia de estos entes matemáticos, deben existir de forma independiente (platonismo) en un tercer reino. Este tercer reino es el del sentido y la necesidad. No sé, a ver que te parece.
Un saludo muy cordial.
domingo 16 diciembre, 2012 @ 2:03 am
La hipótesis de que todo fuese una simulación no se puede afirmar ni descartar con el estudio propuesto: aunque llegásemos a esos límites no hay razón para decir que son pixels o bits de un holograma.
Los temas que se están debatiendo son muy estimulantes.
Amigo tomás:
A mi me da la impresión de que estás en la línea del realismo (materialista y determinista) y no del idealismo, pero prefiero que lo aclares tu mismo.
El amigo lluís también parece estar en la línea del realismo.
Por otra parte, quiero darle mi bienvenida a danielperes: es evidente tu entusiasmo y me ha gustado mucho el talante con el que has entrado. Morin tiene muchas cosas interesantes y me encanta el planteamiento desprejuiciado que propone de cara a la educación…
domingo 16 diciembre, 2012 @ 2:29 am
Morin propone una actitud más libre de prejuicios, pero advierte que somos al mismo tiempo hombre-racional y hombre-demente, que seguimos aferrados a los Dioses y las Ideas. Esto supone un gran lastre para librarnos de los prejucios que nos acompañan, y es algo de lo que ya he hablado en toras ocasiones: el caracter intuitivo (no racional) del cerebro. En mi òpinión, una forma excelente de hacer frente a los prejucios es de la mano de la Ciencia: el prejucio de una hipotética superioridad o inferioridad racial se desmonta con el conocimiento de nuestro origen común en África, con los estudios cromosómicos (que han revelado que nuestras diferencias no son esencialmente genétcias sino culturales); el prejucio de que ser rico puede hacerte más feliz también ha sido falsado; se ha demostrado que la colaboración es la única estrategia evolutivamente estable (también corroborado por filósofos como Sober), etc, etc.
El cerebro funciona de forma principalmente intuitiva, no hace un examen detallado, sino que se basa en tres o cuatro aspectos de índole más bien artística para apañárselas. Y hay que decir que en unas ocasiones consigue resultados sorprendentemente certeros y rápidos y otras lo hace rematadamente mal. Son buenos ejemplos de esto último las ilusiones ópticas, como las que había en la página que nos recomendó tomás hace unos días; también el hecho de que podamos asociar una caricatura a un personaje cuyo físico dista mcuho de ser el retratado en la caricatura. El cerebro se maneja con conceptos absolutos «esta persona es buena», «este otro es malo»…no le interesan los análisis profundos, y renunciará a acordarse del nombre de una persona que acaba de conocer, pero en los primeros segundos ya ha eleborado un juicio intuitivo de dicha persona, que hará que cuando la vovamos a ver no recordemos su nombre pero permanecerá el recuerdo de la sensación que nos produjo (el jucio incial no ha cambiado).
domingo 16 diciembre, 2012 @ 3:08 am
Este cerebro intuitivo, limitado por el número de sus sentidos y sus prejucios, nos lleva a que sólo podamos aspirar a conocer unos pocos aspectos de la realidad. Al explicarle a un ciego lo que es una manzana no podemos recurrir a describirle su color, en la misma línea, David Chalmers hace una analogía con el descubrimiento del electromagnetismo, que sólo pudo empezar a comprenderse cuando se desarrollaron nuevas leyes electromágneticas que considerasen aspectos como la carga y la fuerza electromagnética hasta entonces desconocidas.
En esa misma situación está el problema de la consciencia que no es observable ni mensurable en contextos experimentales.
Es oportuno lo que señala lluís, porque si lo que se propone es intentar implantar la consciencia en un ordenador con bits de silicona es sumamente probable que vayamos al fracaso: en los ultimos años se está empezando a estudiar la influencia de mecanismos cuánticos a nivel cerebral, cosa mucho más cuestionable es si un computador cuántico podría simular ese gran misterio que es el cerebro.
Por otra parte quisiera puntualizar el comentario de que «el sistema vivo es autónomo del ecosistema o sociosistema». Si lo ha dicho Morin me parece completamente gratuíto porque los seres vivos y el ecosistema están codeterminados, en nigún caso son independientes sino codependientes, aquí puedo poner miles de ejemplos, pero no me quiero extender.
domingo 16 diciembre, 2012 @ 8:28 am
Estimado «danielperes»:
Me atribuyes más capacidad de la que tengo cuando me pides una respuesta a tan debatidas -desde siglos- cuestiones.
Dices «… y que tienen el valor de verdad» y también «… son verdaderos o falsos… » deduciendo o afirmando seguidamente «… porque los entes matemáticos existen». Quiero puntualizar que esto sucede, es decir que existen dentro de un determinado campo conceptual que nos hemos dado.
Imaginemos una diminuta Tierra, del tamaño de una canica. poblada por seres racionales de la medida de bacterias. Y sea que, por la pequeñez de su mundo, les fuera imposible percibir la línea recta. Quizá -y recalco que sólo quizá-, no sé hubiera concebido la geometría euclidiana. Hubieran construido directamente la geometría esférica, donde no se puede cumplir el teorema de Pitágoras. Es muy posible que más tarde hubieran concebido la línea recta y el plano euclidianos, pero en el periodo intermedio no contarían con esa herramienta. El mismo caso sería si el tamaño de nuestros cuerpos fuera tan grande que puestos de pié advirtiésemos inmediatamente la curvatura terrestre incluso rodeados de montañas. Con esto quiero decir que existen problemas que pasan por largos periodos desde que nos damos cuenta de ellos hasta que encontramos la solución, o una solución satisfactoria.
Entonces digo que aquello que realmente existe son los acontecimientos, como nos enseña la relatividad, -de todo esto mi docto amigo «lluís» te puede decir mucho más que yo-. Entre unos y otros acontecimientos existen relaciones que, posiblemente, a veces describimos con el lenguaje vulgar,luego afinamos más y les aplicamos la lógica y, buscando la exactitud los tratamos matemáticamente. Otras veces se construye un cuerpo de axiomas y después se aplica donde la realidad admite su aplicación.
Con todo eso quiero decir que podemos idear un sinfín de lenguajes, otro de sistemas lógicos y una infinitud de sistemas matemáticos que nos permiten describir la realidad y comunirnosla entre los seres humanos -y en algún nivel con otros seres no humanos-, pero que esas relaciones nos preceden y seguirán existiendo cuando ya no estemos y que un tremendo número de ellas quedarán sin descubrir, pero algunas seguirán cumpliendo unas leyes que hemos tenido la fortuna de descubrir, o sólo de aproximarnos a su exactitud. Y para esa descripción nos han sido útiles las matemáticas muchas veces y otras no hemos encontrado un cuerpo de ellas aplicable.
Por tanto el concepto de verdad matemático tiene, para mi, el mismo valor que el de verdad lógica. Es deductivo; está contenido desde el principio en el sistema pensado. Y sin el hombre no existiría, aunque las relaciones que explica -con el fin de poder aplicarles el calificativo de verdad- sí existen con independencia de si son explicadas o no.
No podemos dar el mismo valor de existencia a una piedra que me entra por los sentidos que a un pensamiento. Y lo mismo sucede con verdad. El concepto de verdad es distinto cuando digo: «esto es una piedra» que cuando digo «dos y dos son cuatro». Por otra parte, una piedra aquí y ahora es un acontecimiento; dos y dos son cuatro no tiene aquí y ahora, así que no es un acontecimiento; es una relación derivada de un acuerdo para utilización de entes participados y aceptados.
Espero haberte satisfecho. Recibe un cordial saludo.
domingo 16 diciembre, 2012 @ 8:52 am
¡Vaya, ya se me ha colado -y por triplicado,como suele- mi buen amigo Miguel Ángel! Y es que comencé a escribir anoche pero, vinieron a verme mi hijo y nieta, así que he continuado esta mañana.
Creo que tienes razón, Miguel Ángel; me considero realista hasta la médula.
Me gustaría ser más breve, pero he de rendirme; la tendencia a la extensión es superior a mí.
Un fuerte abrazo.
domingo 16 diciembre, 2012 @ 8:08 pm
Se supone que el teorema de Pitágoras, como otros teoremas, son válidos en todo el universo. Pero ocurre que cualquier afirmación matemática más allá de las hipótesis iniciales, axiomas y postulados, tienen la misma o menor validez que éstos. Y la validez de un axioma o un postulado se funda en la confianza que nos prestan los sentidos, incluido el que llamamos sentido común. No obstante, el Universo nos suele dar pruebas de que su lógica no es nuestra lógica, lo que nos llevaría a poner en duda hasta la validez de nuestras más sencillas afirmaciones, incluídas las que contiene este post. Saludos.
domingo 16 diciembre, 2012 @ 8:52 pm
Muchas gracias por tu bienvenida Miguel Ángel, es un verdadero placer estar aquí. Permíteme que puntualice lo de que «el sistema vivo es autónomo del ecosistema o socioecosistema». Sí, lo dijo Morin, pero refiriéndose a la dependencia respecto del medio. Es decir, al ser el sistema vivo un sistema abierto su autonomía depende del exterior (a través del intercambio de energía y materia), de tal forma que se produce una paradoja: más «autonomía» implica más dependencia, pues se necesita más energía del exterior para seguir manteniendo «en pie» la complejidad de la estructura viva. No tiene más importancia. Supongo que ya lo sabes, pero en el segundo volumen de «El método» Morin explica esto mil veces mejor que yo. De nuevo gracias, y espero poder intercambiar más reflexiones contigo.
Estimado Tomás, me dices «me atribuyes más capacidad de la que tengo cuando me pides una respuesta a tan debatidas -desde siglos- cuestiones», y sin embargo creo que tu comentario es una aproximación muy buena. Aunque es cierto que son cuestiones milenarias y abiertas a debate. Creo que has expuesto una versión interesante de lo que Leibniz denomino tipos de verdad: verdades de razón y verdades de hecho. También creo que hemos explorado interesantes vías en relación al realismo y al problema de la simulación y las matemáticas. No quisiera insistir en disputas semánticas sobre el realismo, pues me extendería de más. Sólo te digo que gracias por tus aportes, reflexionaré sobre la cuestión y espero que podamos volver al tema en algún post futuro.
Un saludo muy cordial.
lunes 17 diciembre, 2012 @ 2:38 am
Estimado danielperes:
No he leído ninguna obra completa de Morin, pero lo conozco desde hace años y tengo algunas pequeñas nociones sobre su filosofía que forman parte de mis cuadernos de notas. Muchas gracias por tu aclaración porque me estaba llevando una impresión equivocada.
Como veo que le tema te encanta, te invito a que leas una argumentación muy curiosa por parte de Mario Bunge que se refiere a los asuntos que estamos tratando. Me parece muy interesante la perspectiva de Bunge, físico y filósofo a la vez, tiene ideas de lo más original.
Te mando un abrazo porque en las nuevas noticias ya veo de qué pasta estás hecho.
lunes 17 diciembre, 2012 @ 3:08 am
Muy apreciado petrus:
Efectivamente, hay una barrera inevitable que se deriva de la suma:
Caos universal + principio de incertidumbre (imprecisión de las medidas) + ilusionismo, subjetivismo y limitaciones del cerebro
Podríamos añadir la imprevisibilidad de las contingencias y el desconocimiento de dimensiones, energías (oscuras o no) y otras entidades que aún no hayamos descubierto.
Aún así, con ese cerebro limitado logramos reorganizar los átomos y hacer cálculos que aún no siendo exactos nos permiten llegar a otros planetas con una fiabilidad muy aceptable. También funcionan las poleas según lo describe la mecánica clásica.
El asunto que quería comentarle también a danielperes es la concepción de Mario Bunge sobre el principio de incertidumbre: dice que podría ser tan sólo un estado de ánimo ¿qué os parece?
Bunge es realista y emergentista (aunque no un emergentista radical porque considera que algunas propiedades de los sistemas emergentes podrían volverse a definir en el marco de una teoría general).
Saludos/abrazos
lunes 17 diciembre, 2012 @ 3:47 am
Amigo lluís:
Es de sumo interés la apreciación que has hecho sobre la «teoría de la información», posiblemente conozcas a Henri Atlan que basa su interpretación de la complejidad en esa teoría de Shannon y Weaver. Aquí un breve apunte sobre Henri Atlan, que ya se que andamos todos mal de tiempo:
http://www.henciclopedia.org.uy/autores/Mandressi/Atlan.htm
Por cierto, esos viajes que me recomendaste que hiciese seguramente no los haga, en parte por motivos ecológicos (no contaminar), en parte porque no le tengo mucha simpatía al avión (me hace sentir como un paquete). Lo que si me gustaría es que te animases a poner algún día alguna canción que te guste (de los años 60 o cuando sea), si te ayuda a fluir estaríamos de acuerdo Epicuro, Buda, Martin Seligman y un servidor.
Un gran abrazo.
Abrazos.
lunes 17 diciembre, 2012 @ 8:05 am
Estimado «petrus» (por tu 23):
El Universo no tiene lógica alguna. La única lógica es la que surge de los seres pensantes que lo habitan.
Un cordial saludo.
lunes 17 diciembre, 2012 @ 10:21 pm
Estimado Miguel Ángel:
Muchas gracias por tus comentarios. Espero que no pensaras demasiado mal de mí. Conozco a Bunge de oídas, pero no he leído nada suyo. A ver si puedo leer algo y te digo, pues esa idea del «principio de incertidumbre» como estado de ánimo parece cuando menos interesante. Además, creo que suscribir una postura emergentista moderada es, hoy, algo bastante razonable. Obviamente, incorporando la cibernética, la teoría de la información y sistemas, la biología, las ciencias humanas en general, etc. en fin, complejidad, que es algo que me interesa bastante (aunque estoy lejos de sostener ninguna postura particular).
Un saludo muy cordial.
miércoles 19 diciembre, 2012 @ 11:30 am
Estimados:
Lo que me ha dejado muy pensativo es la frase del artículo: «No tenemos suficientes átomos en el Universo para simular la autoorganización de todos los átomos del propio Universo».
Por lo demás el tema del artículo y todo lo que pueda escribirse sobre si nomos o no una simulación de realidad, me tiene sin cuidado pues, simulación o no, es mi realidad.
Saludos.
miércoles 2 enero, 2013 @ 9:32 pm
Querido amigo tomás:
Lo de que no haya suficientes átomos en el Universo para simular la autoorganización de todos los átomos del Universo va al hilo con una preguntilla que hice en esta página hace algún tiempo. La pregunta era si la Ciencia había desmentido que fuese posible algo semejante al «demonio de Laplace».
Puede que me esté precipitando en mi conclusión, pero diría que algo así sólo es posible imaginarlo desde el punto de vista teórico…y en cualquier caso tendría que ser algo monstruoso.
Abrazos desde la incertidumbre.
viernes 4 enero, 2013 @ 9:02 am
Querido amigo Miguel Ángel:
Concretamente preguntas ¨si la ciencia ha desmentido que fuese posible algo semejante al «demonio de Laplace»¨. Yo no creo que la ciencia pueda desmentir ni confirmar algo así porque, simplemente, no es de su incumbencia. Yo utilizaría el sentido común, o si quieres, podemos llamarle filosofía científica. Para empezar el significado de ese demonio es, en sentido moderno -y para mí- que, conocidas todos los entes existentes, todas las variables y todas las leyes que los relacionan, dado un estado cualquiera del Universo en un momento dado, podría predecirse cual sería un estado futuro e incluso un estado pasado. Este sería mi enunciado. El de Laplace está muy anticuado, aunque tú, ya precisas referirte a «algo semejante».
Ya ves que se trata de un imposible. Primero porque nunca podremos afirmar que conocemos todos los entes, tampoco que conocemos todas las variables y tampoco que conocemos todas las leyes. De cada uno de esas tres cuestiones podremos afirmar que conocemos unas cuantas, pero nunca podremos saber si conocemos todas.
Ahora bien, añades «desde el punto de vista teórico», lo cual quiere decir algo así como «en el supuesto de que eso fuera posible», es decir, sí conociésemos la totalidad de las tres enumeradas cuestiones.
Pues yo diría que tampoco, por una ley que sí conocemos y que vamos a dar por buena: la velocidad finita de la luz y que no hay otra mayor. Supongo conoces la figura de los «conos de luz». Impiden que llegue información desde el exterior de ellos. Por tanto yo diría que el «demonio de Laplace» sólo sería teóricamente posible si la velocidad de la luz fuese infinita. Esto, combinado con el determinismo causal lo haría posible; como digo, sólo teóricamente.
Ya me gustaría que Neo o «lluís» u otro de nuestros muy preparados compañeros diesen una mejor opinión o, para mi ego globular, confirmasen la mía. Con ese ruego, porque el poco tiempo -ese enemigo mío que, aun siendo escaso, con ello quiere destruirme, y yo negarle la existencia- me despido de tí y me dirijo a ellos si me leen antes de que esta noticia se cierre.
Un fuerte abrazo y perdón por no haberte respondido antes.
viernes 4 enero, 2013 @ 9:38 am
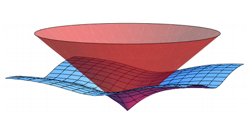
Por cierto que al volver, caigo en la figura ilustrativa del artículo. En ella está el cono del futuro según la representación clásica y, afortunadamente, la representación en un plano curvado del espacio. El vértice es el observador en el presente. Pero ¿y si ese observador fuese el Universo? ¿Cómo representar ese espacio? Imagino que la única forma sería considerar la extensión del Universo hasta allí donde ya no existiera curvatura.
A veces considero un universo ínfimo, por ejemplo considerando sólo cinco estados, consecuentes de muy pocos entes, variables y leyes. Sean los estados A, B, C, De y E. Cada uno es causa del anterior, pero ¿y si A pudiera ser efecto de E? Estaríamos ante un Universo cíclico. Ya se que, según las leyes de la termodinámica eso no es posible, pero ¿y si existiera otra fuerza, tipo gravedad que deformase el espacio a mayores distancias? Porque -es mi opinión- que también las otras fuerzas deforman el espacio, aunque con alcances ínfimos, excepto el electromagnetismo.
Es un especular.
viernes 4 enero, 2013 @ 9:42 am
Me he visto obligado a poner De en vez de sólo la cuarte letra del alfabeto porque el filtro me rechaza diciendo que pongo «d». Y no comprendo la razón. ¿Qué tiene de malo esa letra? Ya me sucedió hace unos días.
lunes 7 enero, 2013 @ 10:05 am
Amigo Miguel Ángel, (amigos Neo y «lluís», please): Nada; ni Neo ni «lluís» responden a la provocación de mi 32. A ti te lo confieso: ¡necesito tanto su opinión! Y es que, en el cono de luz, al hacerse la velocidad infinita, la superficie del cono habría de coincidir con la superficie que representa el espacio. Por tanto podría sacarse, en imposible supuesto, una fotografía holográfica de todo el Universo, una instantánea tridimensional.
Y el tiempo, esa falacia, mi irreconciliable enemigo, pasa sin detenerse. Y la noticia se cerrará. Al deducir el tiempo de una relación hemos creado un monstruo que nos acabará: es el dios de la ciencia.
Un fuerte abrazo.
martes 8 enero, 2013 @ 1:13 am
Bueno, pues si no tenemos la suerte de que nos comente algo Neo, yo sólo te puedo servir de entrenamiento:
Es cierto lo que comentas de que no conocemos todas las variables ni disponemos de todas las leyes. Te agradezco esta aseveración porque me da pie para retomar la visión de Bunge en cuanto al Principio de incertidumbre y en cuanto a la Mecánica cuántica en general.
Bunge pone el ejemplo de lo que ocurre al describir una partícula subatómica: lo único que conocemos es su vida media, su masa y en qué partículas se descompone. Desconocemos las demás variables.
También hablas del vértice del observador…¡puff! el asunto del observador es otra cuestión sin resolver. Volviendo a la MC, la doctrina de la Escuela de Copenhage considera que:
«Si el sistema se encuentra en un estado que es autoestado de uno de los observables correspondiente el autovalor «A», entonces cando el observador mide ese estado observable obtiene con certeza el valor «A».
No soy ningún experto en matemáticas ni en MC y me da igual que la formulación matemática de esta doctrina lleve la firma de monstruos como Bohr, Born, Heisemberg, Dirac y von Neumann…todo esto huele a patraña:
-Se dice que el operador es observable y medible, lo cual ya me parece altamente cuestionable
-Se dice que el observador obtiene con certeza el valor teórico: esto no es cierto, porque ya sabemos que en cada medida hay un margen de error.