Resuelven el misterio de los círculos de hadas
Un modelo matemático sugiere que los círculos de hadas del África austral no serían más que patrones emergentes que aparecerían de manera natural debido a que las plantas compiten por el agua en condiciones áridas.

|
La Naturaleza es a veces sorprende y nos pode delante enigmas que no siempre son fáciles de resolver. En Namibia, Angola y Sudáfrica se da un fenómeno curioso conocido como “círculo de hadas”.
Este fenómeno consiste en paisajes de praderas de hierba tachonados de círculos aislados en donde no crece nada en sus interiores y que en muchas ocasiones están rodeados por hierba alta. Los círculos pueden alcanzar un diámetro de hasta 10 metros. Son estables y pueden permanecer durante décadas, así que no son fruto de la casualidad. Además, se ha podido ver que cuanto más áridas son las condiciones mayor es el tamaño de los círculos.
Se han propuesto varias hipótesis para tratar de explicar este fenómeno, pero ninguna de ellas era hasta ahora satisfactoria. Tampoco se sabía por qué se forman círculos y no otro tipo de formas.
C. Fernandez-Oto, de la Universidad Libre de Bruselas, y sus colaboradores aportan ahora una posible explicación al fenómeno. Según estos expertos, todo se debería a la dinámica de ese ecosistema. Para ello han implementado computacionalmente un modelo simple no lineal de la ecología de las plantas que está basado en premisas realistas (para los curiosos mencionar que se parte de una ecuación de tipo logística).
Su modelo proporciona predicciones cuantitativas que, según ellos, explican el fenómeno. Esta aproximación proporciona una relación entre interacciones no locales fuertes entre plantas y la formación de círculos estables. Los círculos no serían más que patrones emergentes que aparecerían de manera natural debido a que las plantas compiten por el agua en condiciones que son más bien áridas.
El modelo se basa en el hecho de que la planta (se asume una sola especie dominante) produce un sistema de raíces en el subsuelo que es varias veces más grande de lo que se ve fuera en la superficie. El sistema radicular determina lo cerca que pueden estar unas de otras sin que se interfiera demasiado en su crecimiento.
Además, asumen que el suelo puede estar en dos estados estables: o bien está uniformemente cubierto por la hierba o uniformemente carente de la misma.
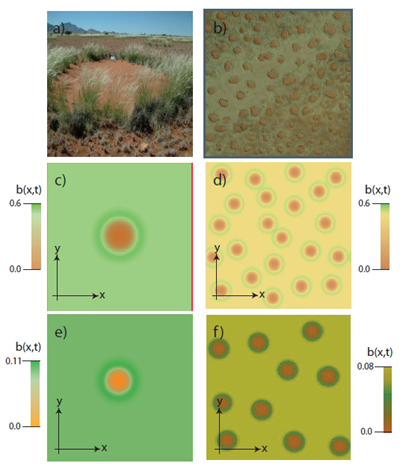
|
|
|
Lo interesante es que ambos estados se pueden dar a la vez en patrones específicos que se corresponden a lo que se observa. El modelo predice que cuando las regiones calvas disminuyen las plantas del borde se acercan unas a otras y sus sistemas de raíces interaccionan entre sí. Pero como las plantas no pueden estar más cerca de lo que el sistema de raíces permite, entonces la reducción del círculo se detiene en un tamaño dado que depende de los recursos disponibles. Como el sistema más eficiente de juntar las plantas bajo estas condiciones es un círculo, entonces aparece esta forma de manera natural debido a la propia dinámica de la ecología de las plantas. En el artículo original se puede ver cómo una forma al azar evoluciona hacia un círculo con el tiempo.
Además, el modelo predice que los círculos deben ser mayores cuanto más secas son las condiciones en las que compiten las plantas. Esto provoca que crezcan sistemas radiculares más grandes y que compitan más entre sí, por lo que deben separarse más. Esto es precisamente lo que se observa en el medio natural.
El modelo matemático es aplicable a otros sistemas que tengan similares características. Es decir, sistemas en los que ciertos elementos compitan entre sí por un recurso limitado en un espacio dado.
Así que, como podemos ver, no hay magia magufa detrás de estos círculos, pese a su nombre.
La Naturaleza a veces es verdaderamente fascinante.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=4147
Fuentes y referencias:
Foto cabecera: Wikipedia.
Artículo original.
17 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





lunes 1 julio, 2013 @ 7:02 pm
…y yo convencido de que los hacían visitantes de Raticulín, ¡qué chasco!
jueves 4 julio, 2013 @ 9:17 am
Pero me pregunto: si las plantas de la periferia ocupasen la superficie calva, ¿no gozarían de más espacio sin interferencia en sus raíces?
jueves 4 julio, 2013 @ 10:08 am
Yo entiendo que estas calvas se sobresaturan de raíces impidiendo el crecimiento de nuevas plantas, las del borde crecen mas al disponer de un sistema radicular mas grande, la competencia entre ellas es lo que proporciona la redondez de las calvas.
Pero ha de haber otros varios factores, probablemente el terreno, el tipo de plantas, el régimen de lluvias, etc. No en todas las zonas áridas las calvas son circulares, es mas yo diría que estas son las mas raras.
Saludos.
domingo 7 julio, 2013 @ 8:50 am
Amigo Pocosé: Creo que tienes razón en el primer párrafo de tu comentario, que es una buena simplificación de la tesis del artículo. Al fin y al cabo el círculo y la circunferencia son la mayor superficie posible dentro de un menor perímetro y allí es donde más espacio van a tener las raíces en competencia.
El que esas calvas sean de otro diseño puede deberse a que ocupen terrenos poco homogéneos en cuanto a humedad o composición, a que estén limitados por plantas de especies distintas y a otros motivos que se complementen para hacer las calvas menos regulares.
Recibe un abrazo circular y con raíces.
domingo 7 julio, 2013 @ 11:38 am
Hay que tener en cuenta que la simetría circular aparece con mucha facilidad en la naturaleza dado que la probabilidad es alta en ambiente isótropos y uniformes y además el agua en reposo es isótropa y uniforme. No sé si dentro de esos círculos » de hadas», aparecen pequeños y casi imperceptibles a simple vista hexágonos, dado que la competencia de los círculos por el espacio plano genera, precisamente, hexágonos.
Por cierto, tomás, el área del círculo y el de la circunferencia son lo mismo, pi por radio al cuadrado.
Saludos.
lunes 8 julio, 2013 @ 8:56 am
Para que se produjeran hexágonos, las calvas circulares deberían estar muy juntas, compitiendo unas con otras. No parece ser el caso.
Saludos.
lunes 8 julio, 2013 @ 9:34 am
Mi querido LLuís: Permíteme discrepar de tu corrección. El círculo es el área interior de una circunferencia y ésta, la longitud que la circunda. Así que el área del círculo es pi por radio al cuadrado y la circunferencia no tiene superficie, pero la longitud de la circunferencia -él círculo no tiene longitud- es dos por pi por el radio.
¡Te pillé! Un gran abrazo.
martes 9 julio, 2013 @ 11:14 am
tomás, el perimetro del círculo es la circunferencia y este perimetro es su longitud, luego el área del círculo está delimitada por la circunferencia.Aunque lo lié un poco y no se entendió bien lo que quisé decir (o lo dije mal).Y desde luego la longitud de la circunferencia no es su área,como bien dices.
Un cordial saludo,tomás.
martes 9 julio, 2013 @ 12:21 pm
Pocosé, me refería al interior de cada calva circular.
Saludos.
miércoles 10 julio, 2013 @ 7:27 am
LLuís, querido amigo, ya sé que ha sido un lapsus y que tus conocimientos están muy por encima de algo tan elemental, pero lo he pasado bien, sin malicia alguna, como puedes comprender dada la muy alta estima y admiración que te reservo.
Recibe un fortísimo abrazo.
miércoles 10 julio, 2013 @ 11:06 am
NO se trata de eso estimado amigo tomás,puesto que mis conocimientos no son nada del otro mundo,lo que en realidad sucedió es que como en tu comentario me dió la sensación, equivocada, de que distinguias entre la superficie de la circunferencia y la del círculo,pues intenté dar a entender que ambas superficie ,despues de todo vendrían a ser lo mismo, porqué comunmente y aunque no sea muy preciso la gente, a veces, suele hablar de área de la circunferencia, cuando en realidad y como tú matizaste bien,se debería hablar de área del círculo.
En fin, estamos aquí muchas veces hablando de la ecuación de Schrödinger, de teorías de campos cuánticos, de supersimetrias, cuerdas y cosas realmente complejas y ahora nos hemos liado con cosas de primaria o casi.
De todos modos considero que ha sido entretenido.
Otro abrazo,querido amigo.
miércoles 10 julio, 2013 @ 5:10 pm
Lluis, tomas, creo que entre pi, el circulo , la circunferencia, y las calvas, creo que es una de las discusiones de blogs mas retorcidamente sanas que hace tiempo veo….:-),,,,,:-),,,,:-),,,
Conclusion: Calva = (cuadrado) elevado a (hada · pi) [eq.1]
¿Os parece ser los 2 peer review para criticar este grandioso descubrimiento?
miércoles 10 julio, 2013 @ 9:21 pm
Dejémoslo en que el área del círculo es igual al área encerrada por una circunferencia cuya longitud es igual al perímetro del círculo antes mencionado. Ese área es A=πr2 en una geometría plana (como en este caso).
En geometrías hiperbólicas o riemannianas sería distinto, claro. ¿Cuál es el área de una patata Pringle? Es una geometría hiperbólica, así que seguro que es un truco para dar menos cantidad de patata por tubo.
Ya puestos, si definimos una función de dos variables que describa la patata, el determinante de su matriz hessiana evaluado en el punto central es negativo. Además los autovalores de dicha matriz en ese punto tienen signos opuesto. Por cierto, el conjunto de los autovalores se llama espectro.
En Mecánica Cuántica los valores permitidos de energía son precisamente los autovalores de un operador (algunas veces definido por una matriz, pero no necesariamente). El conjunto de esos valores es también un espectro. Cuando se trata del potencial culombiano de un átomo y un electrón óptico entonces las diferencias de esos valores de energía producen un espectro de luz visible.
La luz es de lo que viven esas plantas africanas, así que así hemos trazado un círculo, esta vez conceptual.
jueves 11 julio, 2013 @ 1:56 am
Queridos amigos:
Sois estupendos. Hemos pasado de la simpática discusión de Lluís y «tomás» al bucle que nos ha regalado Neo haciendo un recorrido por la geometría hiperbólica y la MC.
Siempre que leo u oigo algo sobre geometría hiperbólica me viene a la memoria el caso de un excelente matemático que quisera compartir como curiosidad. Tenía un gran dominio de las lenguas (hablaba 9 idiomas, entre ellos el chino), la esgrima y el violín. Pero acabó engrosando la lista de perdedores de la Ciencia porque su trabajo sobre geometría no euclídea había sido publicado unos años antes por Lobachevski. Deprimido, acabó por dejar las matemáticas…me estoy refiriendo a Jànos Bolyai:
http://es.wikipedia.org/wiki/J%C3%A1nos_Bolyai
En un episodio de la serie «La Historia de las Matemáticas» comentaron que la única imagen que nos había quedado de Bolyai era un dibujo que aparecía en un sello de correos de la época. Pero debieron equivocarse, porque aunque ese mismo dibujo aparecía en la página de wikipedia hasta hace poco, habréis podido ver que ahora aparece un retrato (creo que es un óleo).
Un cariñoso recuerdo, junto con todo mi reconocimiento, para todos esos perdedores en cuya lista podríamos incluir a Leibniz o a Perelman…o a Nikola Tesla, un científico atípico por haber trabajado en tantos campos que en este aspecto sólo lo podemos comparar con Da Vinci y que, sin embargo, murio sin un céntimo porque siempre se topó con algún Edison, algún Marconi o algún inversosr sin escrúpulos dispuesto a aprovecharse de su indiscutible genio.
jueves 11 julio, 2013 @ 9:21 am
¡Qué bueno, qué extraordinario humor científico el que despliega nuestro magnífico Neo! Una pena que no pueda conocer mi cabeza, más propia para el asunto que su patata, pues goza de una extensa calva exenta de raíces y por tanto imposible de confundir con un campo de hadas. ¡Pero creo que en su interior pululan iones, electrones y seres así, aún más encantadores que las mismas hadas -por sus extrañezas, claro-!
No tenía noticia de Bolyai, querido Miguel Ángel. Mil gracias por tu envío.
Abrazos para todos sin olvidar a mi buen en-amigo LLuís.
jueves 11 julio, 2013 @ 11:16 am
Todos los comentarios generados por la pequeña discusión,tomás-lluí;surgida de una (mí) equivación, recuerdan un poco al «juego de la vida» del matemático John Conway, hemos ido de la simplicidad a la complejidad (representada por el comentario de Neo y) y de paso hemos aprendido algo nuevo, lo del truco de la geometría «Pringeliana», para dar menos patatas por tubo (harina de patata ,aparte de otras sustáncias, en realidad)y lo del matemático al que hace mención Miguel-Ángel del que nada sabía.
Ha sido muy entretenido todo,fresco y gratificante.
En cuanto a eso de en-amigo, tomás, no sé, yo lo simplificaría, quitando el en-.
Saludos a todos.
viernes 12 julio, 2013 @ 8:28 am
Por supuesto querido amigo LLuís. Una pequeña broma que, en puridad, ha de querer decir algo así como «que te siente amigo» aunque juegue con el significado contrario.
Un fuerte abrazo.