Nuevas soluciones al problema de los tres cuerpos
El mismo equipo chino que encontró más de mil soluciones al problema de los tres cuerpos encuentra 231 más.
|
Casi ningún físico se dedica a investigar sobre Física Clásica y menos en Dinámica Celeste, pues se supone que está ya todo dicho.
Uno de los problemas clásico de la Mecánica Celeste fue el problema de los tres cuerpos. Este problema trata de la integrabilidad de la ecuación diferencial que determina las órbitas de tres cuerpos bajo la fuerza newtoniana de gravedad mutua.
Henri Poincaré ya demostró en su día que el problema de los tres cuerpos no puede resolverse por el método de las cuadraturas o integrales de movimiento, a diferencia del caso para dos cuerpos. De las 18 integrales de movimiento solo 10 pueden ser resueltas por las leyes de conservación.
Por tanto, se sabe que no existe una solución analítica general para ese problema, pues la ecuación no es integrable. No se puede determinar analíticamente, para cualquier instante, las posiciones y velocidades de tres cuerpos de cualquier masa que están sometidos a atracción gravitacional mutua y partiendo de unas posiciones y velocidades dadas. No hace falta decir que conforme aumenta el número de cuerpos la situación se complica aún más.
Sí hay soluciones analíticas a problemas de tres cuerpos restringidos, como cuando se asume que una de las masas es despreciables y se asumen órbitas especificas o posiciones fijas.
El problema tuvo y tiene implicaciones una tanto filosóficas, pues incluso sin la influencia de cuerpos externos, el Sistema Solar (que tiene más de tres cuerpos) podría desestabilizarse por sí mismo súbitamente y todo acabaría debido al caos determinista.
Este es un problema que ha mantenido ocupado a los físicos durante 300 años en distinto grado, pero ha quedado un tanto abandonado en pos de la Física Moderna desde hace más de un siglo. Sin embargo, incluso a finales del siglo XX y en este, algunos físicos se han atrevido a abordarlo y encontrado alguna solución particular. Así, por ejemplo, han logrado encontrar algunas soluciones analíticas particulares para ciertas configuraciones, como la que encontró Cris Moore (Santa Fe Institute) en 1993 y en las que dos de esos tres cuerpos ocupan los centros de un ocho y el tercero traza una órbita a lo largo de ese ocho.
Obviamente siempre se puede resolver el sistema numéricamente para cualquier configuración de condiciones iniciales. En 2013 Suvakov y Dmitrasinovic lograron encontrar 13 nuevas órbitas periódicas por métodos numéricos que pertenecían a 11 familias.
La situación cambio cuantitativamente el año pasado cuando investigadores de la Universidad Jiaotong de Shanghai en China lograron encontrar 1223 nuevas familias soluciones, más del doble de las que se habían encontrado en los tres siglos anteriores. En total encontraron 1349 familias divididas en siete grupos dependiendo de su simetría algebraica o geométrica.
Este logro se consiguió gracias al ensayo en un supercomputador de 16 millones de posibles órbitas y a una nueva estrategia numérica denominada CNS (Clean Numerical Simulation).
Todas estas órbitas son periódicas y cerradas. Es decir, cada objeto de los tres empieza la órbita en donde ha dejado la anterior. Además, no se permiten colisiones entre los cuerpos. Son precisamente estas características lo que les hace ser soluciones interesantes y lo que les da importancia. Es decir, buscaban ese tipo de órbitas. Además, las órbitas debían ser planares, los cuerpos tener la misma masa, momento angular total cero y unas condiciones de partida en configuración de triángulo isósceles colineal.
Alguno de estos casos podría encontrarse en la realidad en sistemas triples de estrellas, por ejemplo. Pero, en general, las condiciones para las que se dan la mayoría de ellas son muy difíciles de satisfacer en la realidad. Así, por ejemplo, es muy difícil que en la realidad dos de los tres cuerpos, o los tres, tengan exactamente la misma masa y todas sus órbitas estén en el mismo plano.
Tampoco comprobaron en su día la estabilidad de las soluciones y pudiera ser que algunas de ellas sufran efecto mariposa y que una pequeña perturbación externa desestabilice todo el sistema al cabo de un tiempo.
La lista de nuevas soluciones era impresionantemente larga y los expertos sostenían que debe de haber un número ilimitado de estas soluciones. Así que no es de extrañar que se hayan encontrado más.
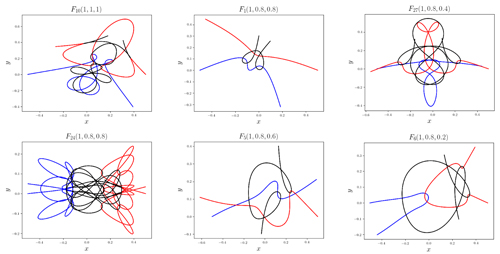
Ahora, este mismo grupo de investigadores chinos (Xiaoming Li y Shijun Liao) ha encontrado 231 casos nuevos casos de órbitas periódicas sin colisiones de 234 presentados, el resto ya habían sido descubiertas por otros investigadores anteriormente. En estos casos han explorado configuraciones en las que las masas pueden ser diferentes y pertenecen a la categoría denominada Problema Pitagórico que se planteo hace más de 100 años por C. Burrau. Algunas de estas nuevas soluciones son complicadas y contienen órbitas en forma de «nudos».
Como en el caso anterior, la posibilidad de que se den en la realidad son muy escasas por no decir nulas, pero no dejan de tener cierta belleza, sobre todo si se las ve en acción en los vídeos. Invitamos al amable lector a explorar estas nuevas soluciones a esta Mecánica celeste imaginaria.
Copyleft: atribuir con enlace a http://neofronteras.com
Fuentes y referencias:
Artículo original 1.
Artículo original 2.
Vídeos con las órbitas encontradas el año pasado.
Vídeos con las nuevas órbitas encontradas.
Gráficos: Xiaoming Li y Shijun Liao.
9 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





miércoles 30 mayo, 2018 @ 11:15 pm
Con independencia de la trascendencia de todo esto, tener (acceso a) los supercomputadores más rápidos del planeta parece que marca una cierta diferencia. Y digo esto sin tener ni idea de qué equipos han usado, pero en cualquier caso, siempre es más tiempo de computación para todos.
Meten mucha y muy pasta, en esto de la ciencia, y la frutería que van a montar va a brillar como nunca en la historia. Al tiempo.
jueves 31 mayo, 2018 @ 1:09 am
Según el artículo original:
This work was carried out on TH-2 at National Super-computer Center in Guangzhou, China.
Que es esta a 33,86 petaflop/s:
https://en.wikipedia.org/wiki/National_Supercomputer_Center_in_Guangzhou
Pero lo más importante es siempre el algoritmo usado. Si este es malo entonces da igual la fuerza bruta que se tenga porque se alcanza el límite muy rápido aunque se tenga la segunda computadora más potente del mundo. Esto es algo que se sabe cualquier que se dedique a métodos numéricos.
En este caso usan un resolvedor numérico de EDO basado en dop853 y, para el resultado, si encaja en lo buscado, se toman las condiciones iniciales que son usadas como aproximaciones a la reales y con un criterio se van corrigiendo las coordenadas y aproximando el periodo por el tradicional método Newton-Raphson. Para evitar la pérdida de precisión usan, además, el mencionado CNS, que se basa en series de Taylor de orden y precisión arbitrarios.
Aunque, como vemos, el método emplea, además de otros, algoritmos de toda la vida conocidos por un estudiante de bachillerato de los de antes, es sofisticado y no se basa sólo en la fuerza bruta.
jueves 31 mayo, 2018 @ 5:22 pm
Supongo que el problema básico queda pendiente…
jueves 31 mayo, 2018 @ 5:51 pm
El estudio de 2013, con sus 13 nuevas órbitas lo vi en su día. Respecto a la posibllidad de que todas esas órbitas sean muy escasas en la realidad,casi con toda seguridad que es así. Las condiciones exigidas para ello son muy «ad hoc», pero como divertimento matemático está muy bien dedicarse al problema de los tres cuerpos ( o ‘n’ cuerpos?. Todo este asunto, la mecánica celeste trajo de cabeza a las mentes mas brillantes de la época de Euler Lagrange, Laplace, Newton y posteriormente Poincaré, siendo este último el que se cargó al demonio de Laplace y por tanto la estabilidad del sistema solar que Laplace estableció con su determinísmo= predictibilidad. Aunque Laplace ya tenía la mosca detrás de la oreja con la establidad del mundo.
Lagrange, ya en 1722 publicó un ensayo sobre el «problema de los 3 cuerpos y me parece que fue el primero en señalar que el problema no podía ser resuelto por integración, mediante una función analítica que fuera solución general de las complejas ecuaciones diferenciales que aparecían al intentar resolver el problema, como sí era posible para 2 cuerpos. Aunque si hubo algunas soluciones en algunos casos concretos, si los tres cuerpos se encontraban en una determinada configuración espacial y al menos dos cuerpos presentaban masas muy grandes con respecto al tercer cuerpo. Euler encontró una solución particular para el caso de que tres cuerpos que se hallaran en línea recta y Lagrange, también encontró una solución particular para el caso de tres cuerpos que se encontraran en los vértices de un triángulo equilátero (los conocidos puntos lagrangianos). No obstante, el propio Lagrange reconoció que las situaciones que esbozó no tenían realidad física alguna, siendo únicamente un divertimento matemático.
Lo que cabe destacar es que esas mentes privilegiadas estuvieran un par de siglos o algo más rompiéndose la cabeza con el problema de los tres cuerpos y sean tan pocos los físicos que se dedican hoy a ello.Aunque se puede entender,quizá sea cosa más de matemáticos a los que importa menos la Naturaleza y más los divertimentos matemáticos, divertimentos que a veces dan grandes sorpresas.
domingo 3 junio, 2018 @ 5:15 pm
Siempre me ha llamado la atención el tema de los eclipse solares totales: el que la luna este «finamente ajustada» para poder producir un eclipse total.
La luna es aprox 400 veces más pequeña que el sol, pero está ubicada 400 veces más cerca, lo que produce que tengan el mismo tamaño aparente.
¿Será posible que la explicación esté en una de las soluciones del problema de los 3 cuerpos?
Así como por efecto marea la luna termina dandole la misma cara a la tierra, es posible que una solución al problema de los 3 cuerpos sol-tierra-luna, termine ubicandola en el punto exacto de cono de luz del sol
martes 5 junio, 2018 @ 10:06 pm
En principio, no (pero quién sabe), porque por transferencia de marea la Luna sigue alejándose de la Tierra. El proceso terminaría en una rotación mutua sincrónica (la Tierra y la Luna mostrándose mutuamente el mismo hemisferio, como Plutón y Caronte), pero no dará tiempo porque requerirá más tiempo del que se tomará el Sol para pasar a la fasr de gigante roja. Aunque nunca se sabe. Es decir, dentro de cientos de millones de años en el futuro el tamaño aparente del disco lunar será menor del solar y sólo se verán eclipses parciales o anulares.
En el pasado, cuando la Luna estaba más cerca de la Tierra, los eclipses duraban más tiempo porque el tamaño aparente del disco lunar era mayor que el solar.
En el sistema solar hay casualidades más sorprendentes. Por ejemplo, cada vez que Venus pasa cerca de la Tierra (es decir, cada vez que nos adelanta «por la derecha»), muestra aproximadamente el mismo hemisferio, de aquí que por radar desde la Tierra sólo se conociera la forma aproximada de ese hemisferio. No tenemos ningún mecanismo que pueda explicar este extraño acoplamiento, si es que es tal cosa.
domingo 10 junio, 2018 @ 7:59 am
El artículo, párrafo 11, habla de la casi imposibilidad de que 2 o 3 de los cuerpos tengan la misma masa y todos estén en el mismo plano. Lo de la masa es realmente mucha coincidencia, pero dos en el mismo plano siempre será cierto en infinitos planos, y tres siempre estarán en el mismo y único plano. ¿Será que se refiere a las órbitas?
domingo 10 junio, 2018 @ 2:02 pm
Solucionado.
martes 12 junio, 2018 @ 9:13 am
Sí. Ahora queda claro. Mil gracias, querido Neo.