Inflación geométrica
Un modelo clásico deducido directamente de la Relatividad General predice una inflación cósmica sin campos extras.
|
La teoría de la Relatividad General (RG) es uno de los mayores logros intelectuales del ser humano. Describe al propio espacio-tiempo como un campo y dice cómo se curva en presencia de masa y energía.
La RG ha superado todas las pruebas a las que se la ha sometido, incluida la colisión de los agujeros negros y la generación de ondas gravitacionales en el proceso. Incluso nuestro sistema GPS tiene en cuenta correcciones relativistas de este tipo para así tener mayor precisión.
Por otro lado, también tenemos la Mecánica Cuántica (MC) que describe el mundo de lo muy pequeño. Pero la RG es una teoría clásica, es decir, que no es cuántica. Además, presenta un problema: cuando retrocedemos en el tiempo con los modelos cosmológicos basados en RG aparecen singularidades. Esto nos dice que la capacidad de predicción de la teoría falla, pues no pueden aparecer esos infinitos. Simplemente se supera el régimen de aplicabilidad de la teoría. Es de esperar que esa singularidad desaparezca cuando se tenga un teoría cuántica de la gravedad, algo que todavía no tenemos.
Por otro lado, el universo observable presenta varios problemas para cualquier teoría cosmológica estandar al uso, como la ΛCDM. Lo que vemos es un universo muy plano, muy homogéneo e isótropo. Estas características no las predice el modelo ΛCDM (un universo con constante cosmológica y materia oscura fría), ni ninguno basado en RG a secas.
Para solucionar esto se introdujo en los años ochenta el concepto de inflación cósmica. Justo entre 10-33 y 10-32 segundos tras la singularidad inicial, el Universo habría experimentado un inflación brutal durante sólo 10-36 segundos. El universo habría multiplicado su tamaño en un factor 1026 durante ese tiempo, algo casi ni imaginable. Esto habría aplanado la geometría y uniformizado el universo que vemos, que pertenecería a una parte minúscula del universo original y que estaba ya en equilibrio térmico. Por eso el Fondo Cósmico de Microondas (FCM) es igual ahora en todas las direcciones en las que lo observemos.
Además de estas pruebas a su favor, quizás en un futuro se puedan detectar los famosos modos B del FCM, puestos ahí por las propias ondas gravitatorias generadas en el Big Bang.
A partir de la época inflacionaria el universo sería descrito por el modelo ΛCDM normal bajo la RG sin ningún problema.
La inflación soluciona así el problema de la planitud y uniformidad del Universo, pero introduce el problema de qué es lo que provocó la inflación cósmica. Hasta ahora se ha supuesto que existiría un campo inflacionario cuya partícula portadora sería el inflatón y que operaría esa escala de energías tal altas. Además de ser una chapuza puesta ad hoc, deja su posible comprobación experimental fuera de toda falsabilidad por los siglos de los siglos, pues ningún colisionador podrá crear inflatones jamás.
Ahora, un grupo internacional de físicos teóricos, en el que participan algunos españoles, propone una solución fabulosa a este problema. A su modelo lo denominan «inflación geométrica».
En la inflación geométrica se produce una inflación sin la necesidad de campos adicionales, ni inflatones, ni nada por el estilo. Sólo usan correcciones clásicas a la RG y pueden ver que la inflación aparece de manera natural al régimen en el que se da el Big Bang y sería un fenómeno puramente geométrico.
Como ellos mismos dicen, la presencia de un época inflacionaria es una consecuencia natural e inevitable de la existencia de una acción efectiva razonable que contiene una torre infinita de correcciones sobre la curvatura a la acción de Einstein-Hilbert de la RG.
Esos físicos parece que han conseguido vislumbrar, sólo usando conceptos clásicos y no cuánticos, una RG corregida para curvaturas muy altas, como las que se dieron durante el Big Bang. Para ello introducen correcciones a la acción de Einstein-Hilbert de la RG de una manera análoga (pero no igual) a cuando hacemos un desarrollo en serie de Taylor. El «primer término» del desarrollo sería la RG y los demás sólo tendrían una contribución no despreciable en un régimen de alta curvatura, siendo prácticamente nulos en el régimen normal.
Es de suponer que una teoría cuántica de la gravedad prediga un comportamiento similar, pero aún no tenemos tal teoría. Sin embargo, este modelo permite predecirlo sólo con aproximaciones clásicas.
La ventaja es que tenemos un modelo, o familia de soluciones, que predice el comportamiento del universo desde el momento 0 hasta el presente de manera continua conectando con el modelo ΛCDM de manera suave y natural.
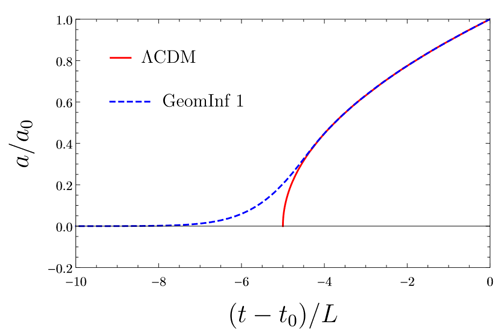
En la imagen de cabecera se puede ver un gráfico en el que se muestra el factor de escala normalizado del universo frente al tiempo. En rojo sería en modelo ΛCDM normal y en azul el de la inflación geométrica. Siendo a0 el «tamaño de universo» en un tiempo posterior t0 para el cual las correcciones de alta curvatura ya no son necesarias. Para este caso y para el modelo ΛCDM, la singularidad inicial se alcanza para t-t0= -5L (choque de la línea roja con el eje horizontal). Pero, cuando se introducen las correcciones de la inflación geométrica, el valor a=0 nunca se alcanza en tiempo finito, sino que esta singularidad es sólo un comportamiento asintótico para t=-∞.
Quizás sea todavía demasiado pronto para asegurar si este modelo es correcto o no, pero, desde luego, es muy prometedor, además de muy bonito. Tampoco parece que hayan todavía realizado predicciones contrastables. ¿Cómo es la generación de ondas gravitacionales primordiales según esto? ¿Dejan alguna señal observable sobre el FCM? Habrá que esperar y ver.
Copyleft: atribuir con enlace a http://neofronteras.com
Fuentes y referencias:
Artículo original.
Gráfica: Gustavo Arciniega y colaboradores.
24 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





martes 8 enero, 2019 @ 10:06 am
Hola don Neo, muchas gracias por el post, es muy interesante. Veo que la publicación es un pre-print de arXiv y es muy reciente, (28 de diciembre). ¿Sabes si los autores han enviado el artículo a alguna revista de Física peer-review para ser publicado?
De nuevo gracias por divulgar Ciencia y Tecnología y ánimos para continuar.
Saludos.
martes 8 enero, 2019 @ 3:01 pm
Estimado Albert:
Los autores que envían artículos al ArXiv normalmente ponen en qué revista se va a publicar, sobre todo si ya se ha aceptado.
En este caso no ponen nada, así que es de suponer que estos estén esperando el resultados de los árbitros de la revista correspondiente. Porque, obviamente, lo deben de haber enviado a alguna revista de prestigio.
Pero es normal que tarde un año o más en ser publicado en la revista oficial. Sea así tal cual o con modificaciones. Puede en entonces sea noticia importante en los medios tradicionales.
martes 8 enero, 2019 @ 7:12 pm
Que no se necesiten campos del inflatón ni sus correspondientes partículas ‘inflatón’ resulta interesante, dado que esos inflatones no pueden encontrarse con acelerador alguno. Pero resulta curioso, al menos para mí, que siendo una inflación ‘geométrica’,lo que casa muy bien con la RG, una teoría cuántica de gravedad pudiera predecir ‘un comportamiento similar’. El frenesí cuántico, con tantos ordenes de magnitud por encima de la ‘suavidad’ del Universo de la RG ¿podrían compaginarse de alguna manera con este modelo de inflación ‘geométrica’?
La falta de predicciones verificables o contrastables, es desde luego, una ‘pega’ que parece importante, a pesar de lo ‘bonito’ del modelo.
Lo que no acabo de ver claro es cómo funcionan esas correcciones a la acción de Hilbert o Einstein Hilbert, ¿tales correcciones modifican de alguna manera las ecuaciones de campo de Einstein o las dejan invariantes?
miércoles 9 enero, 2019 @ 8:01 pm
Estimado Lluís:
Un método estándar en Física es construir una acción y minimizarla. La solución correcta corresponderá a ese mínimo e incluso se puede obtener el comportamiento del sistema aunque no se tenga la teoría completa siempre y cuando podamos obtener esa acción. Suele ser una integral sobre un lagrangiano y este una combinación de la energía potencial y cinética.
Para este caso se parte de una generalización de la acción habitual en RG que incluye el caso habitual. Además obligan a que, entre otras cosas siga la cosmología de Friedmann-Lemaı̂tre-Robertson-Walker (ver apéndice del artículo original). Pueden obtener unas ecuaciones de Friedmann generalizadas. No deducen algo equivalente a G=8πT, pero sí unas ecuaciones de campo que describen la situación con precisión arbitraria según meten más correcciones a la curvatura.
jueves 10 enero, 2019 @ 6:22 pm
Si, ya me fije que se trabajó sobre ese principio de acción mínima, o acción, esa S que aparece en la ‘fuente’. El comportamiento del sistema aunque no se tenga la teoría completa debe ser consecuencia de que tal principio está dentro de la física clásica o newtoniana, pero en lugar de utilizar a Newton por comodidad se echa mano de la mecánica analítica (lagrangiana, hamiltoniana), es válido por tanto, dentro de la RG o en teoría cláscia de campos, electromagnetismo, por ejemplo, y aunque en esos campos la lagrangiana y la acción tomen formas bastante distintas(matemáticamente, considerados), el concepto de mínima acción debe ser el mismo. Por lo visto el Universo es bastante gandúl, prescindiendo de la mecánica cuántica.
Gracias, por la aclaración, Neo. Me ha hecho encajar algunas cuestiones.
domingo 13 enero, 2019 @ 8:06 pm
Hombre, gandul no. Es coherente. Y consistente. Algo que nosotros no somos.
Aquí la pregunta de díptero escrotal obvia es, ¿y cómo nadie vio esto antes? Evidentemente, nadie buscaba inflaciones antes de los 80, pero sí después. La respuesta tentadora, claro, es, «porque andaban echando la caña donde pensaban que había más peces». No deja de ser otra columpiada de las mías con aterrizaje de primera comunión (o sea, con oblea), dado que para sostener este exabrupto debería informarme detalladamente sobre los pormenores y verificar mis hipótesis, pero como todo el mundo avanza sus paridas de una forma u otra, pues cabe plantearse cómo hubiéramos gestionado nuestros recursos si a) esto se revela correcto y b) lo hubiéramos sabido, pongamos, hace 20 años.
Pero bah, así como ha ido también es divertido. A fin de cuentas, la ciencia es trascendente. Y todo lo demás, pues lo será también, pero de forma menos agarrable. Creo que me explico. O no.
lunes 14 enero, 2019 @ 9:58 am
Yo corroboraría que «o no», o sí, o cualquiera sabe. Por mi parte ni me atrevo a abrir la boca ante nuestros sabios; «solo sé que no se nada», pero ni de eso estoy seguro; ¿o sí?
martes 15 enero, 2019 @ 8:14 pm
Pregunto : ¿ quiere esto decir que es posible que el momento de la singularidad inicial del Big Bang se podría retrotraer a menos infinito?
miércoles 16 enero, 2019 @ 3:13 am
Querido amigo Tomás:
Es que te empeñas en aprehenderlo todo desde el pensamiento crítico, pero las singularidades de lo inabarcable no pueden comprenderse sin la ayuda de una buena bola de cristal…
https://twitter.com/Strambotic/status/1082000498235002881
…Para opinar con mucha más solvencia.
miércoles 16 enero, 2019 @ 8:39 am
Eh… Parece claro que sí, que difiere con el dr.Einstein no en varios puntos, sino en vastas (y hasta bastas, incluso de bastar) geometrías al completo. ¿Cómo se llamaba aquella ley de la II República, la de vagos y maleantes? No deja de ser sorprendente la abrumadora cantidad de peña que caería bajo los supuestos de tal ley (bastante desafortunada en su concepción y aún mucho peor en su desarrollo, pero para la gracieta sirve), actualmente. Esta señora, de pleno.
Y saber, saber, algo sabemos, claro, si lo comparamos con el infinito de la ignorancia sabemos pues nada, esa frase cuando era pequeño pensaba genuinamente que la había inventado Sócrates (no Diógenes, el del síndrome, a ese pobre hombre también le habrían clavado la susodicha ley añadiéndole el supueso «los que se dedicaren a recopilar desperdicios, objetos inútiles obsoletos (mira, un museo), y otros fetiches mentales a tal punto que el cúmulo ponga en riesgo la salubridad pública») como respuesta a los interrogatorios de la Inquisición Ateniense, resulta que no, la puso como tantas otras Platón (en boca de Sócrates), este señor me cae gordo (lo era, muchísimo) por varias razones, entre ellas que para no saber nada pontificaba de todo y repartiendo carnets (como Aramís), y además por ser anticientífico hasta el tuétano (que él retorcía dándole la vuelta como un guante), creo que es el caballerete del cual nos queda constancia documental como el más antiguo que percibió, muy correctamente, el efecto dinamita que la ciencia (y la de ellos, muy próxima a la nuestra) tenía para su modelo social la chusma abajo – los que montamos a caballo arriba. Se podía haber ido a correr la espartatlón que para su sobrepeso le hubiera venido mortal de necesidad. O no.
miércoles 16 enero, 2019 @ 10:52 am
Muy simpática la relación que me has mostrado entre Aramís y Einstein, aunque no los veo como posible pareja sexual, querido Miguel: demasiada carne fofa para tan pocos huesos desgraciadamente hace tiempo inermes.
En cuanto a Dr., he de decirle que el infinito de la ignorancia ha de ser cero. Así que afirmo «o no». Todo ¿o nada? es contradicción. ¿Sí o no?
miércoles 16 enero, 2019 @ 11:32 pm
Contradicciones y paradojas, una cosa es que seamos capaces de enunciar conceptos filosóficos como «todo»-«nada»-«infinito» , y otra que los podamos comprender, querido Tomás.
Y de acuerdo en tu valoración sobre Platón y Sócrates, querido Dr. Thriller, apreciando yo también en el último su escepticismo irónico y el método dialéctico.
Abrazo-ós.
jueves 17 enero, 2019 @ 11:21 am
Querido Miguel: Si, más o menos, podemos definir o enunciar, podemos comprender. Y digo «más o menos» porque, en realidad, comprender por completo en profundidad y extensión no nos es posible ni aun en la cosa más nimia. Así, echando mano de las matemáticas más intuitivas, podemos acogernos a los conjuntos y decir que el todo absoluto es eso, un conjunto que abarca cuanto existe, se piensa, etc., de modo que no pueda darse algo fuera de él, de forma que abarque incluso lo desconocido. Pero, eso sí, queda como desconocido, aunque incluido en el todo.
La nada es similar, pero a la inversa. Es el conjunto nulo, donde no es posible incluir algo por sutil o inabordable que sea.
En cuanto en los infinitos, los conocemos de varias clases y de todos, -o quizá solo casi todos- tenemos una idea e incluso podemos manejarlos, que no abarcarlos, como su propio nombre indica. Aunque, ya es importante la gran cantidad de conceptos que no permiten aplicárseles tal denominación. Ello nos faculta para no ser tan ajenos a su naturaleza; es decir que no nos sean totalmente imposibles de comprender.
jueves 17 enero, 2019 @ 3:56 pm
Espero que no sea una tontería.
Entiendo el infinito que tiende para más, (por ejemplo, el de los números Naturales). Como CONJUNTO CON LIMITE, solo que, este LIMITE no es estático, todo lo contrario, este LIMITE seria DINÁMICO, de tal forma que cuanto mas nos aproximamos de él, más se va apartando. Pero ojo, sin dejar de ser cerrado.
Tratándose de conjuntos matemáticos abstractos, este concepto en la práctica en nada difiere del concepto tradicional aceptado para infinito.
Ya en situaciones de Espacios con realidad objetiva (con energía/materia/campos …) sí que tiene diferencia, pues, aunque su LIMITE no lo consigamos alcanzar, sí que la densidad de ese espacio ira diluyéndose conforme corremos atrás de su LIMITE. Este iría creando en su camino inexorable, el ESPACIO REAL OBJETIVO.
viernes 18 enero, 2019 @ 11:28 am
Amigo Eduardo: No creo que sea una tontería lo que dices. Es una opinión más o menos compleja, pero en absoluto una tontería.
No estoy de acuerdo con tu primer y segundo párrafos. Si tomamos los números naturales y escogemos todos los que están compuestos por una cifra, ese será el conjunto finito; si consideramos hasta tres cifras, lo mismo, pero siempre finitos; incluso podemos definir el conjunto solo de todos los que tienen cinco cifras, excluyendo los que tienen menos y los que tienen más. Son conjuntos finitos y, a la vez, subconjuntos de un conjunto infinito. En realidad, para la definición de un conjunto finito usamos el de los números naturales estableciendo una relación biunívoca: a cada elemento del conjunto que sea le hacemos corresponder uno de la serie de los números naturales. Por ejemplo al conjunto «piedra, papel, tijera» le hacemos corresponder con {1,2,3}. Entonces, el conjunto infinito lo pensamos, por oposición, con aquel que no podemos establecer tal relación, pero tú sabes como construimos el conjunto de los números naturales, por inducción, por lo que tiene principio, pero no fin, siendo, por tanto, infinito. Además, dentro de este conjunto infinito, caben subconjuntos infinitos (según mi parecer); por ejemplo dentro del conjunto infinito de los naturales, cabe el subconjunto infinito de los pares. O el de los impares y dentro de este el de los primos, pero hay el doble de naturales que de pares o impares y el de los impares incluye al también infinito de los primos más el dos; es decir que existe la intersección del elemento 2 de los primos en el subconjunto de los pares. La cosa se aleja mucho más de tu visión de simple alejamiento si nos metemos en el campo de los números reales, porque ¿cuál sería el siguiente o el antecedente -es decir los correspondientes de los naturales- al número «e», al «pi» o al 2^(1/2)? Incluso es infinito el conjunto entre el «e» y el («e»+1). Por todo ello no puedo estar de acuerdo con esos dos párrafos.
El tercer párrafo no creo comprender lo que escribes. No sé si ese LÍMITE persigue la nada -«densidad que irá diluyéndose»- como final de lo infinito de una realidad que lo integra todo, incluso construcciones mentales -campos de fuerzas-. Lo siento, pero no lo entiendo.
Un abrazo… final (al menos del comentario)
viernes 18 enero, 2019 @ 8:16 pm
Tomas.
Buena la explicación que haces sobre el infinito a través de los conjuntos.
Entiendo que ese concepto de conjunto infinito que explicas se aplica únicamente en un Espacio Matemático, por tanto, Abstracto e Insubstancial.
Intuyo que según dices, este conjunto matemático. Por ejemplo, el de los números Naturales es infinito, porque al hacer una correspondencia biunívoca con cualquier conjunto de objetos reales, aunque sea este último muy grande (todos los átomos del Universo) siempre sobraran números Naturales) por tanto el conjunto real de átomos no es infinito. ¿A no ser que el Universo también sea infinito, quién sabe? Aunque para eso tendría que constantemente ir apareciendo substancia Nueva.
Es por eso que digo que en este caso el infinito seria DINÁMICO, su último término siempre estaría avanzando, (nuevo átomo)
Entonces partiendo del PRINCIPIO (por tanto, postulado, premisa a gusto) de que la energía/materia del Universo es limitada (fija), no puede existir ningún infinito en él.
Seguramente objetaras que el Universo podría ser infinito ya de por sí, desde siempre. ¿Puede que así sea, quién sabe?
Volviendo al Espacio Matemático Insustancial Abstracto, este por definición ya es infinito, por tanto, no se aplican las anteriores limitaciones.
Pero creo que debemos ir con cuidado al formular estructuras matemáticas (modelos) en este Espacio Matemático, para entender el comportamiento de los fenómenos en el Universo Real.
En la inmensa mayoría de fenómenos naturales existe una casi total correspondencia entre las previsiones de los modelos matemáticos y los fenómenos reales, pero no en todas, como en el caso de las Singularidades la violación de simetría CP, o la ausencia de antimateria.
Creo que esto es debido a que el Espacio Matemático es mucho más RICO, más amplio, tupido y constante, en su estructura abstracta “puntos” que el Espacio del Universo Real.
Este concepto de “punto” también creo que tiene su miga.
Un abrazo casi infinito
viernes 18 enero, 2019 @ 9:49 pm
Ehm… Tengo que puntualizar que la ausencia de antimateria es hipotética. Se basa en la obviedad de que, evidentemente, si una galaxia de materia se tropieza con otra de antimateria los fuegos artificiales estarían más allá de toda imaginación (también valen simples nubes moleculares), como tal fenómeno no se observa se infiere que todo el universo observable es de materia, al que hay que sumar que el consenso da por hecho que el comportamiento gravitatorio de la antimateria es idéntico a la materia (hay fuertes indicios de que así es, pero no está probado ni mucho menos).
Claro, si ahora resultara que la antimateria tiene un comportamiento gravitatorio anómalo (por soltar la columpiada, que se repela), pues creo que ven con claridad las implicaciones. Mucho me temo que esto no va a ser así, pero la verdad estaría bien. En el sentido de la fiesta. Que se iba a montar.
viernes 18 enero, 2019 @ 10:00 pm
El infinito de la ignorancia ha de ser cero… Pues, sí, así debería ser, sin embargo, cuanta más ignorancia tanto más ruido. De fondo y de primer plano. ¿Será un efecto Casimir? No debería, porque ignorancia y osadía son fenómenos independientes.
Eso espero.
M.A., uno de los filósofos más simpáticos fue Descartes. Aparte de segregar para siempre «ciencias» y «letras», resulta que me entero que venía de Touraine, la provincia francesa del Ancien Régime donde estaba lo que hacía las veces de TC y hasta la Revolución la variedad particular de Oïl de aquel país era tenido por lo más sublime de la corte (hasta que París ocupó ese nicho con Ggobespiegga), en otras palabras, como Descartes hablaba fisno y no patán no veas la de puertas que debía abrirle. Cuando me tragué su hagiografía en el insti de esto no me dijeron ni mu. Y seguro que el mamoneo que se traía con la sueca incluía logopedias francófonas.
viernes 18 enero, 2019 @ 10:01 pm
El infinito de la ignorancia ha de ser cero… Pues, sí, así debería ser, sin embargo, cuanta más ignorancia tanto más ruido. De fondo y de primer plano. ¿Será un efecto Casimir? No debería, porque ignorancia y osadía son fenómenos independientes.
Eso espero.
M.A., uno de los filósofos más simpáticos fue Descartes. Aparte de segregar para siempre «ciencias» y «letras», resulta que me entero que venía de Touraine, la provincia francesa del Ancien Régime donde estaba lo que hacía las veces de TC y hasta la Revolución la variedad particular de Oïl de aquel país era tenido por lo más sublime de la corte (hasta que París ocupó ese nicho con Ggobespiegga), en otras palabras, como Descartes hablaba fisno y no patán no veas la de puertas que debía abrirle. Cuando me tragué su hagiografía en el insti de esto no me dijeron ni mu. Y seguro que el merengue que se traía con la sueca incluía logopedias francófonas.
domingo 20 enero, 2019 @ 6:27 am
¿Lo de «simpático» es literal, o lo dices con retintín, Maese Dr. Thriller? Tengo entendido que el propósito principal de sus «Meditaciones metafísicas» era socavar el ateísmo.
martes 22 enero, 2019 @ 6:01 pm
Con retintín, ma non troppo. Y bueno, Descartes tampoco era el tipo de persona amante de la revolución… En fin, desde el Renacimiento en general el panteón hagiográfico de los Grandes Franceses tiende a destacar a personalidades si no teniéndolas, deseosos de tener comodidades y confort personal en su modus vivendi. No es que otros panteones les guste destacar sujetos próximos al masoquismo y vida Diogénica (alguno hay), pero el francés hace particular hincapié, se regodea, vamos. Si no, no me explico cómo pueden tragar (en realidad no lo hacen) como inmenso pedagogo y hasta cuasi pediatra al tipo que enchufó a todos sus bastardos en la inclusa. Más allá de resaltar extracción social, se entiende.
Serán traumas del insti.
miércoles 23 enero, 2019 @ 4:35 pm
Desde mi infinita ignorancia y osadía, por tanto, esta última libre de prejuicios contaminantes del conocimiento formal actualmente aceptado, expondré lo que pienso al respecto de este tema.
No me preocupa el ridículo, creo que vale la pena exponerse a este, ante la posibilidad, aunque remota, de que esclarezca algo el tema. Mejor que la cobardía de quedar callado.
Seguramente no tiene nada nuevo, pero por si acaso allá voy.
Partiendo del concepto del ESPACIO MATEMÁTICO como un conjunto infinito abstracto e insustancial. Sus elementos serian PUNTOS sin dimensión. Entre ellos se pueden establecer cualquier tipo de relación matemática… líneas, planos, superficies, volúmenes. distancias…. Etc., conocidas y por conocer.
La primera dificultad que encuentro al pensar en este espacio es:
Si sus elementos son PUNTOS y estos no tienen DIMENSIÓN espacial…. como pueden tener alguna identidad… ser ELEMENTOS, ser algo a usar como referencia? Creo que si les damos alguna identidad (posición individual) automáticamente deben tener dimensión… la que sea.
De lo contrario, sin dimensión automáticamente se evaporan (desaparecen), y por lo tanto también el concepto de Espacio Matemático. Por otro lado.
Imagine el conjunto de los números Naturales. 1,2,3,4,……..n…………En el intervalo entre por ejemplo el 227, y el 228, no puede existir un conjunto infinito de puntos matemáticos, pues al ser infinitos, estos no podrían estar separados, terminarían fundidos, constituyendo un CONTINUO, con lo que también perderían su identidad como PUNTOS (elementos del conjunto).
Se puede argumentar que, el Espacio Matemático sea de esta forma, un CONTINUO, pero entonces nos encontramos con la dificultad de como podemos trabajar con este continuo, si en el no podemos hacer marcas con PUNTOS por estos no tener dimensión.
Según estas dificultades, solo se me ocurre que, en este Espacio Matemático Contino, solamente podemos trabajar con pedazos de CONTINUO, o sea regiones (nubes), con CONTORNO, tan extremamente pequeñas como sea necesario, para aquella estructura matemática en estudio.
Creo que estas dificultades no existen en el Espacio Real de Nuestro Universo, (con sustancia) pues desde Planck aceptamos que este está cuantizado, entiendo que no puede existir en el cualquier elemento menor que la Escala de Planck. (Dimensión de Planck)
No por eso debemos abandonar el concepto de Espacio Matemático de PUNTOS, pues constituye una formidable herramienta de trabajo para entender la Realidad de Nuestro Universo, pero sí ser conscientes de sus limitaciones.
Gracias.
miércoles 23 enero, 2019 @ 8:41 pm
Desde el punto de vista matemático entre por ejemplo el 227 y el 228 existe un conjunto infinito de puntos matemáticos y constituyen un continuo, pero los puntos no pierden su identidad.
viernes 25 enero, 2019 @ 10:21 am
En efecto, así lo veo, maestro Neo. Siempre tan juntos como queramos, pero con su propio valor o posición.