NeoFronteras

Utilizan una computadora bacteriana para saber si un grafo es o no hamiltoniano. Esto sería una demostración para un nuevo tipo de computación.

Grafo hamiltoniano con uno de los posibles ciclos hamiltonianos marcado. Foto: Wikimedia C.

Quizás algunos de los temas más interesantes en la ciencia son los asuntos interdisciplinares, cuestiones que unen más de una rama del saber. Si a usted, amigo lector, se le dice que las Matemáticas pueden aplicarse a la Biología o a la Genética seguro que no se sorprenderá demasiado, al fin y al cabo las Matemáticas son el lenguaje de la ciencia. Pero, ¿y si es al revés?, ¿y si es la Genética la que ayuda a resolver problemas matemáticos?
Todo aquel que realmente esté interesado en la Informática (es decir, más allá de jugar con el ordenador y bajarse material de la red) sabe de la importancia de la Matemática Discreta. Esta rama de las Matemáticas permite estudiar la naturaleza de los números y, por tanto, desarrollar sistemas de cifrado, como el RSA que le permite conectarse de manera segura con su banco. Nos dice también la manera de encontrar una solución óptima a un problema, como la ruta más corta entre dos puntos. Los lógicos que han trabajado en problemas computacionales nos dicen que hay problemas muy duros de computar, de tipo NP o NP completos, que básicamente no pueden ser resueltos de manera óptima en un tiempo razonable. La única manera que tenemos (o la única posible que existe) para resolverlos de manera segura es enumerar todas las configuraciones posibles y escoger la mejor. Es decir, aplicando fuerza bruta. Pero los ordenadores tienen sus limitaciones a la hora de resolver los problemas a base de fuerza bruta si el sistema a resolver es lo suficientemente grande, pues el tiempo de resolución crece exponencialmente, aunque sea un hipotético ordenador cuántico.
Es aquí donde la Biología puede ayudar. Podemos tener un cultivo de miles de millones de bacterias que genéticamente computen lo que nosotros queramos. O, al menos, esa es la idea.
Recientemente unos investigadores norteamericanos han creado una “computadora bacteriana” capaz de resolver un problema matemático sofisticado (aunque pequeño), demostrando así que es posible realizar computación en células vivas y abriendo la puerta a diversas aplicaciones. Esta segunda generación de computadoras bacterianas ilustra además la capacidad de este método para resolver de manera real problemas matemáticos complicados.
El equipo de investigadores, pertenecientes a diversas instituciones científicas, usaron ingeniería genética para modificar bacterias E. coli que fueron capaces de resolver el problema conocido como problema del ciclo hamiltoniano. Este resultado es una extensión de sus trabajos previos con este tipo de computación, y con el que anteriormente resolvieron el “problema de la tortitas quemadas”, resultado que ya cubrimos en NeoFronteras.
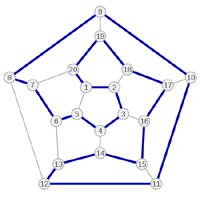
El problema del ciclo hamiltoniano pregunta sobre si en un grafo, formado por diversos vértices unidos por aristas, hay una ruta que empezando por un vértice se vuelva al mismo pasando una sola vez por cada uno de los otros vértices, aunque se queden aristas sin visitar. Es decir, si así es el grafo será hamiltoniano y si no es así no será hamiltoniano.
Aunque hay algún criterio (como el de Dirac) que permite decir en algunos casos si un grafo es hamiltoniano, no hay, en general, un criterio universal que nos lo asegure, a diferencia del caso de decir si un grafo es o no Euleriano (si tiene o no un camino que partiendo de un vértice visite todas las aristas una sola vez). La ausencia de tal criterio frustra a muchos estudiantes de informática que estudian Matemática Discreta como parte de su formación, pues, pese al parecido, los conceptos de grafo euleriano y hamiltoniano son muy distintos. La mayoría de las veces la única manera de decir si un grafo es hamiltoniano es encontrar un ciclo* hamiltoniano en él.
Estos investigadores modificaron el circuito genético de las bacterias E. coli para que fuesen capaces de encontrar un ciclo hamiltoniano en grafos de tres vértices (por pequeño un problema ridículamente simple por otra parte). Las bacterias que resolvieron satisfactoriamente el problema informaban por fluorescencia roja y verde simultánea, produciéndose colonias amarillas.
Aunque el problema es en este caso simple, lo importante de este resultado es que nos dice que es posible resolver este tipo de problemas. Su extensión a grafos mayores sería factible.
La Biología Sintética es el uso de las técnicas de Biología Molecular, Ingeniería Genética y modelización matemática para diseñar y construir circuitos genéticos que permitan a las células vivas realizar nuevas funciones. Según uno de los autores este resultado es un ejemplo más de lo poderosa y dinámica puede ser la Biología Sintética. En este caso se ha usado para resolver un problema matemático, pero se puede aplicar a Medicina o a investigación sobre fuentes de energía, Medio Ambiente, etc.

Fuentes y referencias:
Nota de prensa.
Jordan Baumgardner, Karen Acker, Oyinade Adefuye, Samuel THOMAS Crowley, Will DeLoache, James O Dickson, Lane Heard, Andrew T Martens, Nickolaus Morton, Michelle Ritter, Amber Shoecraft, Jessica Treece, Matthew Unzicker, Amanda Valencia, Mike Waters, A. M. Campbell, Laurie J. Heyer, Jeffrey L. Poet and Todd T. Eckdahl. Solving a Hamiltonian Path Problem with a bacterial computer. Journal of Biological Engineering.
Computador bacteriano resuelve problema.

* Para ser precisos si el grafo admite un ciclo (volver al mismo vértice de partida) es hamiltoniano, si admite un camino (sin volver al mismo vértice de partida) entonces será semi-hamiltoniano. No será ni una cosa ni la otra si es imposible visitar una sola vez todos los vértices.