NeoFronteras

Según unos investigadores si se vacuna periódicamente y al ritmo adecuado se puede detener una epidemia incluso si hay pocas vacunas disponibles.

Virus de la gripe A. Fuente: Harvard School of Public Health.

Ahora que parece que la gripe A no va a diezmar la población mundial y, por tanto, se puede hablar sobre el tema de las pandemias sin parecer sensacionalista o “conspiranoico”, podemos tratar un resultado reciente sobre este asunto. Curiosamente no versa sobre Biología Celular, Genética, anticuerpos o diseño de vacunas, sino sobre la dinámica de las epidemias y su modelización matemática.
Quizás los lectores no saben que el tema de las pandemias se viene investigando desde hace años para así adoptar protocolos de actuación (al menos en los países civilizados) para el caso de que llegue alguna. Los humanos representamos el mayor caldo de cultivo que haya existido jamás para virus y bacterias oportunistas. Las leyes de la evolución nos dicen que tarde o temprano, sobre todo a esta tasa endiablada de reproducción humana, surgirá un microorganismo que diezmará la población.
No es ciencia ficción, porque ya pasó varias veces en el pasado, como con la peste negra, la conquista de América, la gripe del 18, el SIDA, etc. Por tanto, es conveniente saber cómo actuar en el caso de que se produzca.
Una opción puede ser no hacer nada, dejar que se reduzca la población mundial y dar así un alivio al planeta y a una civilización que de otro modo perecerá víctima de su propio hiperconsumo y estulticia. Como ésta es una lotería a la que probablemente pocos quieran apuntarse, puede que sea mejor idear medidas que eviten la tragedia. Cerrar colegios y centros de enseñanza, reenfocar el transporte público o usar mascarillas pueden ser estrategias válidas, sobre ellas se han realizado ya estudios.
Un trabajo bonito se hizo sobre un juego que algunos efectuaban con billetes de curso legal. Básicamente, el juego (Where’s George) consistía en seguir la pista en Internet a unos billetes de dólar (sobre los cuales se sabían sus números de serie) para así saber adónde viajaban. Los datos fueron utilizados por un grupo de investigadores para ver cómo se podrían propagar las epidemias.
Tradicionalmente se asumía que, de algún modo, aparecía un brote de una enfermedad en un lugar y a partir de él se extendía la epidemia, pero el juego de los billetes demostró que el transporte moderno (sobre todo el aéreo) hacía que aparecieran muchos brotes casi simultáneamente en muchos lugares. Así que la situación actual es mucho peor de lo esperado.
Algunos matemáticos se han dedicado a construir modelos de propagación de enfermedades o (como en el caso que vamos a relatar) al estudio de protocolos sobre modelos que nos digan qué estrategia es mejor a la hora de vacunar a la población.
Un caso lo hemos visto recientemente en España con la gripe A. La vacuna iba a llegar tarde y no había unidades para toda la población. Así que se decidió vacunar sólo a un porcentaje de la población (inferior al de otros países), principalmente a grupos “de riesgo”. Cuando esto se supo empezaron a surgir colectivos que reclamaban su derecho a ser vacunados. Al final, cuando se vio que no era tan grave, ha pasado lo contrario y muchos (probablemente influenciados por teorías de la conspiración) defienden su derecho a no ser vacunados.
Pero esta situación puede que se dé tarde o temprano de nuevo. Puede que no haya tiempo de fabricar vacunas suficientes, entonces ¿qué estrategia seguir?, y ¿cuándo y cómo realizar dicha campaña de vacunación? Una buena campaña debe de salvar vidas, pero también tiempo y recursos.
La intuición nos dice que para parar la epidemia cuantos más individuos se vacunen rápidamente mejor. Si vacunamos simultáneamente a todos la enfermedad simplemente desaparece. Pero no siempre se tiene la capacidad de utilizar la fuerza bruta.
Michael Khasin, de Michigan State University, y sus colaboradores sugieren una estrategia basada en modelos matemáticos. Según ellos, una campaña adecuada, aunque limitada en el número de vacunas disponibles, puede evitar la pandemia, pero sólo si se realiza de la forma adecuada.
Según ellos es posible acelerar la erradicación de una enfermedad contagiosa con una serie de vacunaciones periódicas. Según ellos, cuando la cantidad de vacunas es limitada esta estrategia es la mejor.
El problema con las poblaciones grandes es que la dinámica de la enfermedad puede dar lugar a un estado en el que una fracción de la población permanece infectada durante mucho tiempo. Esto es el resultado de un proceso aleatorio de infección y reinfección, que también depende de la tasa de recuperación y la tasa de defunciones. Este ruido o fluctuaciones residuales hacen que exista siempre esta infección residual.
Las fluctuaciones más grandes pueden hacer, sin embargo, que la enfermedad desaparezca por completo. A veces lo hace de manera espontánea, como ejemplo tenemos la enfermedad del sudor inglesa, que aterrorizo a la Europa de los siglos XV y XVI y que desapareció mucho antes de que llegara la ciencia moderna para identificar al microorganismo responsable.
Pero, precisamente, así es cómo debe actuar una campaña de vacunación: provocar una gran fluctuación que con un poco de suerte haga que la enfermedad entre en una tasa de extinción exponencial.
Estos investigadores han estudiado cuál sería el protocolo de vacunación óptimo que permitiría entrar en ese régimen. Según ellos lo ideal es una serie de microcampañas o pulsos de vacunación periódicos.
Llegaron a esta conclusión al darse cuenta que el protocolo de vacunación óptimo sigue una solución de un problema variacional de minimización de acción sobre un sistema Hamiltoniano (en este caso sujeto a la condición de la tasa promedio de vacunación). Para el que no entienda el lenguaje de la frase anterior, sólo decirle que se trata de un problema típico en Física.

La trayectoria más probable en el modelo estocástico SIR de individuos susceptibles de infección (X1) frente a infectados (X2), ambos reescalados para N (población total). La línea a trazos muestra una trayectoria determinista hacia el estado endémico y la línea continua muestra, a partir de ese punto, la trayectoria más probable que da lugar a una extinción de la epidemia inducida por una fluctuación. Fuente: Michael Khasin.

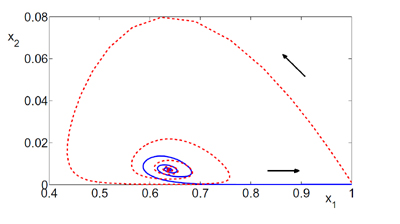
Lo mejor de este resultado es que es independiente del modelo usado (para una tasa de vacunación pequeña en promedio). Lo malo es que el efecto perseguido depende fuertemente de la frecuencia a la que se producen los pulsos de vacunación, sobre todo para el caso no estacionario en el que una población estocástica está modulada periódicamente en el tiempo.
Para poder entrar en ese régimen de extinción exponencial antes mencionado hay que administrar los pulsos de vacunación para que se ajusten a la frecuencia propia de oscilación que modula la enfermedad (en teoría una frecuencia específica para cada enfermedad). Sería algo así como entrar en una especie de “resonancia negativa” para la cual el sistema decae exponencialmente.
Si la frecuencia de pulsos de vacunación no se ajusta a esa frecuencia propia, entonces el resultado obtenido puede ser incluso peor y que la epidemia se extienda aún más.
De manera intuitiva lo podemos visualizar como que el número de infectados, pese a fluctuar, tienden ser mayor o menor por oleadas periódicas. Si justo cuando se da uno de los extremos vacunamos a la población contrarrestamos la dinámica del sistema, al igual que cuando detenemos poco a poco un niño que se columpia.
El resultado puede ser interesante, pues no siempre se dispone de muchas vacunas a la vez, son perecederas o tienen un efecto limitado en el tiempo por culpa de las mutaciones de los agentes infecciosos. Aunque quizás sea más difícil averiguar la frecuencia propia de la epidemia que desarrollar una vacuna para la enfermedad que la causa.

Copyleft: atribuir con enlace a http://neofronteras.com/?p=2960

Fuentes y referencias:
Artículo en ArXiv.