NeoFronteras

Desarrollan un modelo teórico de nanomotor que, de implementarse experimentalmente, superaría los límites clásicos de la Termodinámica.

La Termodinámica experimentó un gran desarrollo en el siglo XIX a raíz de la revolución industrial, sobre todo cuando se trataba de estudiar la máquina de vapor o los motores de explosión interna.
Esta rama de la Física es posiblemente de las más sensatas y se comprende bastante bien si se desea.
Entre otras cosas nos dice que la energía va perdiendo calidad durante su uso de tal modo que cada vez es menos posible realizar un trabajo. La energía de calidad se va transformando en calor y se va generando entropía, que es una medida del desorden de los sistemas. La entropía en un sistema cerrado siempre aumenta, frase que constituye una de las formas de enunciar el segundo principio de la Termodinámica.
Un sistema cerrado termina termalizando hasta una temperatura dada con un máximo nivel de entropía y ya no se puede producir trabajo.
El calor es una forma de energía que pasa de un lugar a otro por efecto de la diferencia de temperaturas. Sólo lo hace espontáneamente de un foco cálido a un frío. Si queremos que lo haga al revés entonces tenemos que meter energía extra desde el exterior. Esto constituye otra de las modalidades de enunciar el segundo principio de la Termodinámica. Vienen a decir que un frigorífico no funciona cuando se desenchufa.
También podemos obtener trabajo cuando en ese paso espontáneo del calor del foco cálido al frío interponemos un motor térmico. Así por ejemplo, la caldera de una máquina de vapor está a mayor temperatura que el ambiente y se puede obtener trabajo que desplace a la locomotora. Es similar para un motor diesel o uno de gasolina (ciclo de Otto).
Cuánto trabajo seamos capaces de extraer en este proceso depende de lo habilidosos que seamos. Lo ideal es que el rendimiento sea lo más alto posible. De este modo, si el carbón de la caldera produce 100 unidades de energía y transformamos en trabajo 10, entonces habrá un rendimiento del 10% o un rendimiento de η=0,1.
Pero, por muy habilidosos que seamos, no podemos mejorar indefinidamente el rendimiento de un motor térmico. Cada tipo de motor tiene un rendimiento máximo que no puede ser alcanzado, aunque nos podamos aproximar a él todo lo que queramos. Además, el máximo rendimiento posible viene dado por la máquina de Carnot.
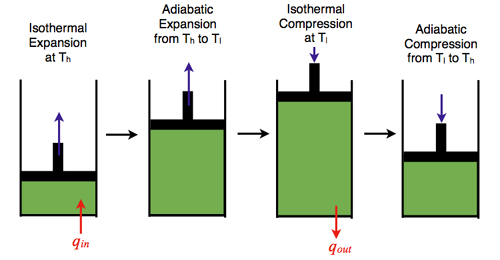
La máquina de Carnot es un motor térmico conceptual basado en el típico pistón con un gas encerrado en el interior y que está conectado a un foco cálido a una temperatura Tc y a un foco frío a una temperatura Tf. Opera con un ciclo en el que sucesivamente dicho gas experimenta una expansión isoterma, una expansión adiabática, una compresión isoterma y una compresión isoentrópica (ver ilustración).
Si se tiene cuidado en los cálculos se puede demostrar que su rendimiento teórico máximo es

η= 1 – (Tf/Tc).

Es decir, el rendimiento dependen exclusivamente de la diferencia de temperatura, cuando mayor sea esta diferencia mayor rendimiento se tendrá. Si, por ejemplo, Tf=300 grados kelvin y Tc=600 grados kelvin, entonces η=0,5, es decir, que el rendimiento es del 50% en ese caso. Se supone que es imposible mejorar este rendimiento.
Este rendimiento es otra forma de enunciar el segundo principio de la termodinámica.
Lo malo es que cualquier otra máquina térmica real tiene un rendimiento muy por debajo del límite de Carnot.
Pero los gases que se consideran en todos estos cálculos son gases ideales y no se considera una discretización atómica. ¿Qué pasa si nos vamos a la nanoescala?
En 2012 un físicos alemanes de las universidades de Mainz y Erlangen-Nürnberg demostraron que si se construyera un nanodispositivo en el que el gas es reemplazado por un solo átomo ionizado entonces podían producir trabajo a partir de dos focos de calor, uno frío y otro cálido. Es decir, se comportaba como un motor térmico.
Además, se dieron cuenta de que algo así podía tomar ventaja de la nanoescala y de los fenómenos cuánticos, como el efecto túnel que operan a esa escala para así superar los límites de la Termodinámica clásica.
La clave está en acoplar este tipo de nanomotor a reservas de energía no térmicas de tal modo que se pueda extraer más energía. Han descubierto recientemente que efectivamente se pueden sobrepasar los límites de la segunda ley de la Termodinámica clásica, porque en este caso se está fuera del equilibrio. Es decir, se puede enunciar una extensión de la segunda ley para un caso más general que el habitual.
El motor propuesto se basa en un foco térmico, un foco no térmico y una propiedad óptica cuántica (squeezing) que ha sido usada experimentalmente antes en diversos campos.
El estudio realizado es puramente teórico, pero en él demuestran que un dispositivo de este tipo tendría un rendimiento realista de hasta dos veces superior al límite de Carnot con dos focos térmicos.
Quizás lo más interesante sea que puede ser realizado experimentalmente con la tecnología actual a partir de un ion y un haz láser. Algo en lo que parece que ya están trabajando.
Si tienen éxito sus resultados posiblemente tengan aplicaciones prácticas en un futuro en el campo de los nanomotores.
A nosotros nos ha servido para repasar un poco de Termodinámicas, que nunca viene mal.

Copyleft: atribuir con enlace a http://neofronteras.com/?p=4327

Fuentes y referencias:
Artículo original.
Copia del artículo original.
Ilustración: UCDavis.