Optimizan la criba de Eratóstenes
Inventan un nuevo algoritmo que ahorra memoria a la hora de implementar la criba de Eratóstenes.
|
Los números primos nos producen fascinación. Esos números que sólo son divisibles por ellos y por la unidad, son los números “fundamentales” a partir de los que se pueden obtener los demás. Los números no primos, o compuestos, no son más que el producto de varios números primos.
Hay algunas conjeturas que van más allá, como la de Goldbach, que sostiene que todo número par mayor que 2 puede obtenerse como la suma de dos primos. Sin embargo, todavía no se ha conseguido demostrar esta conjetura. Tampoco se ha demostrado que sea falsa, pues no se han encontrado contraejemplos pese a que se ha explorado hasta números muy grandes.
Se ha tenido más éxito con la conjetura débil de Goldbach que sostiene que todo número impar mayor que 5 se puede obtener como suma de tres primos, como 3 + 3 + 5 = 11 o 19 + 13 + 3 = 35. Esta conjetura fue demostrada en 2013 después de 271 años por matemático peruano Harald Helfgott (Universidad de Göttingen).
Pero este matemático no se ha conformado con esto y ha desarrollado un algoritmo que mejora la criba de Eratóstenes para encontrar números primos, que es del año 240 AC. La versión de Helfgott reduce mucho el uso de memoria de computador y puede, por tanto, reducir el tiempo de ejecución de un programa que busque números primos.
Eratóstenes era un astrónomo, matemático y geógrafo que además fue director de la biblioteca de Alejandría. Es famoso por calcular el tamaño de la Tierra.
Hace 23 siglos se disponía poco más que el conteo de pasos para medir distancias. Pero ya se habían inventado las Matemáticas y, además de la Aritmética, se disponía de la Geometría. En esa época Eratóstenes midió los pasos entre lo que es la actual Asuán en Egipto y Alejandría (u ordenó a alguien para que lo hiciera o copió el dato oficial disponible).
Durante el solsticio de verano el Sol proyecta sombras verticales en Asuán a mediodía, así que los rayos del sol son verticales y, en época, Eratóstenes podía medir al ángulo relativo del Sol en Alejandría durante el solsticio de verano midiendo la sombra proyectada por un palo (usó probablemente en realidad un cuadrante solar o algo similar).
Eratóstenes sabía que la Tierra era redonda, como cualquier persona instruida de la época, y se propuso medir el tamaño de este mundo usando esos datos, su intelecto y un poco de geometría. Si la unidad de medida fue el estadio egipcio (no se está seguro de este punto, pues pudo ser el estadio griego el usado) el matemático, astrónomo y geógrafo logró medir un valor para la circunferencia terrestre de 39.614,4 km frente a los 40.008 km reales, valor que arroja menos de un 1% de error relativo. A la hora de calcular la distancia a la Luna fue menos afortunado y calculó que había 123.280 km en lugar de los 384.400 km reales. Para la distancia Tierra-Sol obtuvo 139.996.500 km frente a los 149.597.870 km reales. Aunque en estos casos las órbitas elípticas no arrojan una distancia fija en el tiempo.
De todos modos, el error que cometió fue muy pequeño dada la existencia casi nula de tecnología de precisión en esa época.
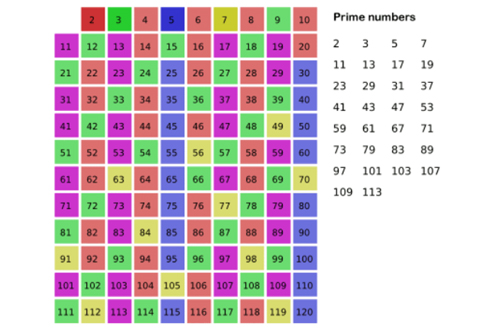
Volviendo al asunto de los números primos, Eratóstenes propuso su famosa criba que permite ir encontrando números primos. De toda la lista de números naturales de un intervalo dado eliminamos primero todos los pares (salvo el 2 al ser primo), pues son múltiplos de 2 y, por tanto, compuestos. Luego los múltiplos de 3 (salvo el 3) y así sucesivamente. En cada paso nos van quedando cada vez menos números a comprobar. Los que van sobreviviendo son primos.
Este procedimiento sencillo puede enunciarse en un algoritmo que puede ser programado en un computador, pero su implementación requiere de mucha memoria. Los ordenadores actuales son muy rápidos y pueden efectuar cálculos en paralelo, pero la memoria siempre representa una limitación para los cálculos.
Para saber cómo de bueno es un algoritmo se deben considerar dos cosas: el número de operaciones por bit del input y el número de bits que hay que almacenar en la memoria mientras que las instrucciones son ejecutadas. La criba de Eratóstenes es relativamente eficiente respecto al número de operaciones a ser realizadas por bit, pues crece en proporción al tamaño del intervalo considerado. Pero la necesidad de memoria crece mucho con el tamaño del intervalo considerado y esto limita la eficiencia de la criba.
Hay otras cribas y algoritmos además de la de Eratóstenes, pero la ventaja de esta es que puede trabajar conjuntamente en la factorización de compuestos, que es la descomposición de un compuesto en producto de primos. Esto de la factorización es algo fundamental en la seguridad de sistema RSA de cifrado de clave pública, pues se basa en la dificultad de factorizar un compuesto formado por dos primos muy grandes. El RSA es el sistema que permite el comercio en Internet y las operaciones bancarias.
Helfgott ha sido capaz de modificar esta criba para que funcione con menos memoria en lo llama “método circular”. Así por ejemplo, para calcular primos en el entorno de los billones, la criba modificada requiere sólo unos pocos millones de bits en lugar de miles de millones que necesita la criba de Eratóstenes tradicional. Es decir, en lugar de necesitar una memoria de tamaño N sólo se necesita una memoria de tamaño raíz cuadrada de N.
Las principales ideas sobre este método se presentaron en julio pasado en XXI congreso de Álgebra Latinoamericano que se celebró en Nuevos Aires y en el Sinapsis 2016 de París.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=5075
Fuentes y referencias:
Artículo en Scientific American.
Esquema: Wikipedia.
24 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





lunes 3 octubre, 2016 @ 12:09 pm
Se eliminan (en criba de Eratóstenes)todos los pares, excepto el 2 que curiosamente es el primer número primo y es par. Y, por definición, el 1 que parecería un primo, pues no lo es.Y es el único primo que no está sólo, o sin que se interponga nadie en su relación con el 3.
En cuanto a Eratóstenes muchos científicos le consideran un verdadero genio, y realmente lo fue. Lo extraño, es que aún quedan «terraplanistas».
lunes 3 octubre, 2016 @ 11:27 pm
Estimado Lluis,
Yo creo que llamar solamente genio a una persona que es capaz de medir la distancia al Sol con un palo o inventar un sistema para encontrar números primos que solo se ha mejorado al cabo de unos 2000 años es quedarse muy muy corto, es curioso que con la riqueza de vocabulario que tiene el castellano no haya una palabra superior.
martes 4 octubre, 2016 @ 12:12 am
Para mí los tres mayores dioses del Olimpo griego son Eratóstenes, Sócrates y Euclides.
Euclides creo que se gana el derecho con su alucinante contribución a la Geometría que todavía usamos hoy en día.
Sócrates por su archiconocido «solo sé que no sé nada», refrendado más de 2000 años después por la incertidumbre de Heisenberg y la incompletitud de Gödel.
Pero mi favorito de todos es Eratóstenes y es por una cosa que comentaba Carl Sagan en «Cosmos»: en la Grecia Clásica se hicieron extraordinarios avances en el conocimiento, pero los sabios responsables de estos avances fueron incapaces de poner en tela de juicio cuestiones como la esclavitud o la creencia de que los griegos eran un pueblo superior.
En esto último Eratóstenes fue casi la única excepción: pensaba que en todos los pueblos y culturas había aspectos interesantes y dignos de consideración. Y eso es lo que le convierte en tan digno de consideración para mí.
martes 4 octubre, 2016 @ 12:49 am
Estimado Lluís:
El 2 y el 3 son primos por méritos propios (he cambiado el texto para mencionarlos, aunque era obvio), pero el 1 no es primo simplemente por definición. De este modo en cada teorema que se mencionen propiedades de primos no hace falta decir «excepto el 1».
martes 4 octubre, 2016 @ 6:49 am
No menor del 2%, querido maestro Neo; menor del 1%. Algo así como el 0,96… %. Muy grande Eratóstenes.
Tantos abrazos como primos.
martes 4 octubre, 2016 @ 11:49 am
Parece que Sócrates nunca dijo eso de » sólo sé que no sé nada». Estuve leyendo unos artículos en los que se argumentaba que nadie puede demostrar que Sócrates dijera eso.
De haberlo dicho, se opinaba en tales artículos, sería una muestra de arrogancia intelectual sobre aquellos que piensan que alguna cosa saben. Una especie de » falsa modestia» que sería una antecedente del «posmodernismo» que se sigue sufriendo actualmente, posmodernismo en el que por ejemplo se concede el mismo valor al vudú que a la teoría de la Relatividad General.
Así que «el sólo sé que no sé nada», sería un «preposmodernismo», que aún se invoca por aquellos que adoptan una especie de superioridad moral para negar la validez de las leyes científicas, o verlas como meros paradigmas cambiantes, según «las modas».
Creo que es mejor decir que sí, que sabemos algunas cosas, pero que aún faltan muchas más por conocer.
Un saludo a todos.
martes 4 octubre, 2016 @ 8:38 pm
Creo que los primos, en realidad, pueden ser considerados una subespecie de los naturales, con algún «gen» defectuoso, probablemente el gen que codifica la proteína de la sociabilidad. Primo es a compuesto como lobo es a perro. Los números primos son insolidarios, solitarios, rebeldes, desordenados, inclasificables, intratables, sin empatía… y en buena parte autistas. Y sin embargo casi todos los genios matemáticos de la historia se han quemado las cejas ( a la luz de las velas, supongo) intentando poner orden en su conjunto. Menos mal que Eratóstenes inventó lo de la criba, sencillo pero que hay que idear, que Euclides nos demostró que no merecía la pena ponerse a contarlos y Gauss los adobó con los logaritmos , domesticando un poco su natural indómito.
Me consta que hasta el aficionado petrus tiene por ahí bastantes páginas sobre ellos y sus malas costumbres, que tal vez acaben viendo la luz en alguna revista o informe de esos que nadie leerá nunca. Si ocurriera, les contaría de qué se trata, pero, parodiando a Fermat, este post es demasiado pequeño para resumirlas aquí… A lo mejor ahora se explican por qué les tengo tan poco cariño. La antipatía es mutua, supongo. Es un decir.
miércoles 5 octubre, 2016 @ 7:04 am
¡»petrus», no seas tan malo! No digo que todo, pero deja por aquí alguna gotita de tus esencias, que será recibida con placer. Venga, hombre…
miércoles 5 octubre, 2016 @ 7:06 am
Querido Lluís: Existen infinidad de frases históricas y famosas que se atribuyen a tal o a cual y, posiblemente, su autor se las asignó a algún importante, bien para darles solera, por modestia o por lo que fuere.
Por mi parte soy incapaz de ver relación alguna entre la esencia del vudú, tan científico y la TRG, tan caprichosa y primitiva, con sus predictoras maldiciones y todo eso.
Pero yéndonos a la frase de marras, ves que resulta una fácil paradoja pues dice «que no sabe nada», pero confiesa que «lo sabe», por lo que algo sabe.
Un fuerte abrazo.
miércoles 5 octubre, 2016 @ 12:13 pm
Sí, eso es cierto, tomás.Quiero decir la cantidad de frases históricas que se ponen en boca de alguien que jamás las pronunció. Einstein es un buen ejemplo de ello.
Volviendo a Sócrates,independientemente de que pronunciara o no esa frase, el problema es el enorme mal uso que se ha hecho y se hace de ella por parte de los tipejos del relativismo cultural, como ya señalé en mi comentario anterior.
Y cómo dijo Wittgeinstein, nada se puede saber de lo que no sabemos; al menos hasta que lo sabemos, si es que llegamos a saberlo,se podría añadir, por tanto decir que » no se sabe nada», no es saber algo, es no saber nada.
En cuanto a los primos,se puede decir que son los «padres» de todos los demás números. Como dice Neo, los números fundamentales, remitiéndose a las conjeturas de Goldbach.Y sí, son realmente fascinantes, su carácter más bien solitario, les da un aspecto entre mítico y «perdedor» que les hace atractivos.
Los solitarios, siempre resultan misteriosos y despiertan curiosidad. Solitario no tiene porqué significar ser huraño.
Un saludo amigo tomás.
jueves 6 octubre, 2016 @ 1:45 am
Pues recuerdo , amigo Lluís, que también nos comentaste que Pitagóras pudo ser también un personaje ficticio y que en realidad lo que había era una academia con ese nombre.
Sobre la duda de la autoría del Principio Socrático, podría ser que la frase sea posterior, una especie de síntesis del modo de pensar de este sabio. Pues le estoy dando vueltas a lo que comentáis del enunciado y, si no contradictorio, cuando menos es fácil de malinterpretar. Vamos, que has logrado sembrarme duda.
Un fuerte abrazo.
jueves 6 octubre, 2016 @ 9:31 am
Querido Lluís:
La aportación de Vittgenstein, por el que siento un gran respeto y he tenido ocasión alguna vez de dialogar en el Museo de la Fundación La Caixa, en su parte primera «nada se puede saber de lo que no sabemos» es tautológica y, como continua con «hasta que lo sabemos…» mejorado por tu añadido, corresponde ya a otro «universo», el de lo sabido, por lo que no afecta a lo desconocido. Así que yo propondría, con modestia, pero intentando escapar de la paradoja y la tautología: «Sospecho que nada sé», como un lema que casi nada entre dos aguas, puesto que una sospecha no es un conocimiento. Mejor escaparía de todo peligro la que propones al final de tu tercer párrafo, de total contundencia y que me atrevo a personalizar para el que hable: «no sé nada».
En cuanto a tu asignación de «personalidad» a los primos es una idea muy atrayente. Me agrada mucho, quizá porque tenga mucho de poesía.
Querido Miguel:
Me parece más correcto llamarle «Método socrático», pero es sólo una de esas manías mías.
Abrazos múltiplos (además de múltiples) para ambos.
viernes 14 octubre, 2016 @ 8:12 am
Querido Neo:
Aunque no haces ni caso a mi 5, me veo en la irresistible obligación de decirte que enuncias mal la conjetura de Goldbach. Debe decir en el párrafo segundo: «… todo número par mayor que 2 puede obtenerse…». Olvidas decir «par».
Mi más sentido pésame y un abrazo, que no es para tanto. Ya sé que soy un tocap… Perdón por ello, dado lo mucho que te has molestado por mí tantas veces.
sábado 15 octubre, 2016 @ 8:20 am
Querido Lluís:
Como es bueno reconocer errores propios, he de confesar que me confundí en mi 12 al contestarte, con el nombre del Wittgenstein -además, sin querer, lo puse con V-. Mil perdones y golpes de pecho, querido amigo. Me refería a Wagensberg, que fué, hace ya más de diez años director del Museo de La Caixa y, muchas veces, asistía a las conferencias. Pero, claro, si estos hombres extraordinarios se hubiesen llamado Lluís o Tomás, no habría problema. Seguro, mi buen amigo, que te darías cuenta de lo anacrónico -Wittgenstein murió en 1951- de mi afirmación, pero tu prudencia lo dejó pasar, lo que te agradezco pero no aconsejo, porque lo que no se corrige permanece, manteniendo el equívoco, y personas poco conocedoras del tema pueden tomarlo como cierto de por vida.
Gracias por tu tolerancia y un abrazo.
domingo 16 octubre, 2016 @ 9:25 am
Queridos amigos, especialmente Neo, Lluís y Miguel que dan la impresión de ser los más adictos a las mates:
Resulta que los primos me traen siempre de cabeza y ello ha llevado a que se me ocurra una demostración de la famosa conjetura de Goldbach tan aparentemente sencilla que sospecho ha de tener algún fallo, puesto que mentes tan privilegiadas se han ocupado del tema sin mucho éxito. Allá va por la vía de la lógica aplicada a conjuntos (lo escribiré sin signos lógicos para que todo lector lo entienda. Además no sé poner los signos con este ordenador; con el otro que tengo, sí):
Premisa 1ª: Todo número par termina en 0, 2, 4, 6 u 8, formando el conjunto P de los números pares.
Premisa 2º: En él, cada número está una sola vez. El 4 está una vez, el 22 una sola vez, etc.; esto es fútil, pero importante.
Premisa 3ª: Al ser todo número primo >2 impar, cualquier suma de dos de ellos, distintos o iguales, ha de terminar en 0, 2, 4, 6 u 8, formando el conjunto S de la suma de dos números primos, ambos >2. (Esto es algo así como el inverso evidente de la conjetura en cuestión)
Premisa 4ª: Sucede que algunos números pares pueden obtenerse por más de una pareja de primos. Por ejemplo: 3 + 7 = 10 y 5 + 5 = 10.
Luego:
El conjunto P está contenido en el conjunto S. Es decir, que el conjunto P de los números pares es un subconjunto del conjunto S de la suma de dos números primos menores que 2. Pero esto significa que todo número par puede descomponerse en la suma de dos primos > 2, que es la famosa conjetura.
Defensa: Todas las premisas son ciertas y también la conclusión.
Problema: ¿No habrá un error en la inferencia; es decir, en el "luego"? Pero no logro ver el fallo.
Agradecería una crítica de cualquiera, haya sido nombrado o no, porque tengo algún argumento de defensa.
Gracias anticipadas a quien se moleste y abrazos para todos.
domingo 16 octubre, 2016 @ 9:39 am
Mil perdones. En el párrafo tras «Luego», pongo «menores» en vez de «mayores», y «».
Y con los perdones y golpes de pecho, más abrazos que nos dejarán «molt prims»
domingo 16 octubre, 2016 @ 9:45 am
Veo que al sistema no le gusta que se le pongan comillas a los signos de > y <. Eso es lo que va en el comentario que ha sido sustituido por "".
¡Ala, más abrazos!
lunes 17 octubre, 2016 @ 1:24 am
Estimado Tomás:
Gracias por señalar las erratas. Ya han sido corregidas.
En cuanto a los posibles móviles perpetuos de primera especie o demostraciones sobre la conjetura Goldbach lo mejor es no dedicarles tiempo.
Los símbolos de mayor y menor están reservados en html para escribir cierto tipo de código, por eso dan problemas aquí. Lo ideal es usar hmtl estricto con la secuencia que empieza por el símbolo &, lt para menor, gt para mayor y cerrando dicha secuencia con un punto y coma.
lunes 17 octubre, 2016 @ 9:22 am
Querido Neo:
Es posible que algún ejercicio intelectual no merezca dedicársele tiempo, pero no es justo, ni siquiera razonable, comparar el móvil perpetuo de primera especie que es absolutamente imposible, al violar la segunda ley de la termodinámica -por lo que no ha podido ser comprobado ni una sola vez, lo que es completamente previsible- con la demostración de una conjetura que hasta ahora ha resultado cierta en los millones de veces que se ha probado sin encontrarle fallo. Por otra parte, me remito al segundo párrafo del artículo: «… todavía no se ha conseguido demostrar esta conjetura. Tampoco se ha demostrado que sea falsa, pues no se han encontrado contraejemplos pese a que se ha explorado hasta números muy grandes». Esa afirmaciones demuestran que esta misma página se ha ocupado en el tema, que algunos matemáticos han trabajado en ello y que quizá se sigue haciendo por otros no incompetentes.
Como tu respuesta me ha parecido inapropiada, he mirado por ahí para informarme y he podido leer que, entre otras mentes extraordinarias, se han ocupado del tema nada menos que Euler -que afirmó la certeza de la conjetura y dijo tener una demostración sencilla que desconocemos-, Cantor, L. Schnirelmann, G. H. Hardy, Vinogradov, Groucho Marx, etc.
Y volviendo al artículo, dedica el tercer párrafo a comentar que, tras 271 años se ha conseguido demostrar la conjetura débil, lo que permite deducir que parece razonable dedicar algunos más a la fuerte.
Y más de una vez, sobre todo aquí, estimado Neo, he podido leer la importancia de ocuparse de la ciencia básica. Mucha más, para mí, que elucubrar sobre la posibilidad de viajar a la más próxima estrella… y no digo a más lejanas, lo que se ha hecho en algún artículo y en comentarios.
De todas formas, si tomo tu respuesta como un consejo, puede aceptarse y hasta agradecerse; lo que pasa es que yo pedía otra cosa: ¿donde está mi fallo si lo hay?
Así que, como consejo, mil gracias.
lunes 17 octubre, 2016 @ 9:38 am
Otra vez querido Neo:
Perdona por haberme fijado solo en el 2º párrafo -porque me ha dolido- y no haberte dado las gracias por tu molestia y dedicación en el contenido de los 1º y 3º.
Sabes cuanto te admiro. Un abrazo.
martes 18 octubre, 2016 @ 10:44 am
¡Caramba «petrus», olvidé ponerte entre los duchos en mates! No me lo explico habiendo leído tu 7, donde dices que «tienes por ahí bastantes páginas sobre ellos» -lo que contradice en cierto modo tu animadversión-.
¿No se te ocurre algo que me diga donde yerro en mi 15?
Por si tengo la fortuna de que me digas algo te voy a exponer ya mi defensa, que es un razonamiento paralelo al ya expuesto:
1º Sea el conjunto C de las combinaciones sin repetición. No importa el orden. (Sería el equivalente al conjunto P de los pares)
2º Sea el conjunto V de las variaciones sin repetición. Importa el orden. (Sería el equivalente al conjunto S de la suma de las parejas de primos > 2)
3º Sean P las permutaciones.
4º Sabemos que V = C x P
Luego:
Todo el conjunto C está contenido en el conjunto V, es decir que C es un subconjunto del conjunto V. Y eso quiere decir que cualquier elemento de C es un elemento de V. (Paralelo a que cualquier par está contenido en la suma de dos primos > 2).
De todas formas, querido «petrus» si no te apetece, influido o no por esa manía que tienes a los primos, puedes ignorar mi petición de ayuda. Si así fuera, ya le escribiría a Euler, que parece ser dijo que tenía una demostración sencilla, además de haber escrito en relación con este tema en una carta a Goldbach: «No creo que sea totalmente inútil plantear aquellas proposiciones que son muy probables aunque falte una verdadera demostración, pues aunque se descubra que son incorrectas, pueden conducir al descubrimiento de una nueva verdad». De esta frase deduzco que no es una tontería buscar una demostración. Lo que me extrañaría en grado sumo es haberla hallado yo.
Un fuerte abrazo aunque decidas no ilustrarme. .
martes 18 octubre, 2016 @ 12:38 pm
Querido Tomás:
Hay mucha gente que cree poseer soluciones a problemas de Matemáticas. Había hace unos años uno que decía poseer una solución racional de pi. Iba por las facultades buscando profesores que le escucharan. En la tele se quejaba amargamente de que no le hacían caso.
También hay «soluciones» al último teorema de Fermat y a muchas otras cosas.
Lo malo es que hay problemas que son realmente difíciles y, además, se sabe que son difíciles, por lo que no merece la pena echar un vistazo a «soluciones ingenuas», entre otras cosas por ser una inmensa pérdida de tiempo.
Todo el mundo tiene derecho a pensar e intentar encontrar soluciones a los problemas. Existen vías para publicar teoremas y similares que son las adecuadas, generalmente revistas del ramo o congresos. Esta web no es ni una cosa ni otra.
Desde hace más de 11 años que en las normas de participación está puesto que no se aceptan ese tipo de cosas. Esto es aplicable a todos los participantes, incluso a los habituales. Pese a todo de vez en cuando aterriza un paracaidista para contar su última teoría definitiva sobre el Universo. Normalmente ni les contesto, entre otras cosas por falta de tiempo.
Además tengo razones personales para no responder a consultas sobre Matemnáticas, porque es lo que hago durante mi jornada laboral y no me apetece trabajar 16 horas al día.
Si se me solicita explícitamente, como usted hizo en su 15, entonces me veo obligado a contestar y a dar la respuesta estándar, aunque no lea su demostración.
Espero que comprenda todo esto.
jueves 20 octubre, 2016 @ 10:37 am
Admirado:
Comprendo -resumiendo- que no tienes tiempo por falta de tiempo.
Espero hayas excusado el haberme dirigido a ti. Ya ves que esta vez no lo hago para que no te sientas obligado. Solo una precisión: yo pedía se me indicase donde estaría mi error porque no lo encontraba y no podía creer haber resuelto la demostración de la conjetura, así que no me siento aludido por tus censuras. Y, aunque, como es natural y educado, he leído con atención cuanto dices, dalo por no leído y quedamos en paz.
Un fuerte abrazo.
viernes 21 octubre, 2016 @ 1:09 am
Es que 16 horas de Matemáticas…¡ni aunque te gusten! Con semejante jornada yo caigo en depresión seguro (ni siquiera aguanté las doscientas y pico horas mensuales cuando trabajaba en el hospital. Eso sí, con turnos de noche que te destrozaban los ritmos circadianos).