NeoFronteras

Dibujo: Delft Outlook.

Por cerca de 150 años los físicos han estado intrigados por el problema de la estabilidad de la bicicleta. ¿Cómo es posible que una bicicleta en movimiento sea estable? Los modelos matemáticos que habían desarrollado hasta esta fecha no eran muy buenos, ahora parece ser que unos investigadores de la Universidad Tecnológica de Delft junto con colegas de Cornell University y University of Nottingham han encontrado el modelo computacional teórico «definitivo» de bicicleta que predice la estabilidad de un diseño dado.
Durante un tiempo toda la Física conocida era Física Clásica, que describía por ejemplo las órbitas de los planetas o los cuerpos en movimiento. Pero a principios del siglo pasado se descubría la Relatividad y la Mecánica Cuántica y ya nuestra concepción del Universo nunca fue la misma. Casi todos los esfuerzos de investigación se volcaron en los nuevos campos de la Física Moderna y problemas de Física Clásica pasaron a un segundo plano, entre otras cosas por ser meramente académicos. O quizás algunos de ellos no eran tan académicos.
Los fabricantes de bicicletas no han sido capaces de explicar con precisión cómo funciona una bicicleta. Simplemente han conseguido ajustar las bicicletas a través de la experimentación directa, sin un modelo matemático que les ayudase a diseñar buenas bicicletas. El resto de nosotros tenemos fe, nos montamos encima y no nos caemos.
Desde que se inventó la bicicleta a pedales, allá por 1860, no se ha dado con una formula o conjunto de ecuaciones que describan un modelo preciso de bicicleta y que prediga bien las características dinámicas de la misma. En los modelos anteriores se tendía a simplificar las ecuaciones del movimiento eliminado varios parámetros, con lo que al final obtenían un modelo poco realista. En este caso se han tenido en cuenta muchos parámetros. Aunque estos investigadores no han aclarado exactamente cómo afecta a la estabilidad cada uno de esos parámetros, sí han podido mostrar cómo lo hacen los principales.
Arend Schwab es uno de los que han participado en el desarrollo del modelo computacional de bicicleta publicado recientemente en Proceedings of the Royal Society (Series A). Explica que su modelo tiene en cuenta veinticinco de los factores o parámetros de los que depende la estabilidad y maniobrabilidad de la bicicleta. El modelo explica además cómo la bicicleta reacciona a una velocidad específica.
Según las conclusiones del modelo, una bicicleta debe rodar entre 14 y 20 Km/h para que sea inherentemente estable. Si va más deprisa oscila menos, pero puede volcar si el ocupante se inclina de lado demasiado. Han podido comprobar que los datos experimentales coinciden con los obtenidos del modelo.
Uno de los factores de los que depende la estabilidad es el efecto giroscópico, cosa que se puede probar colocando plomo en el borde las ruedas. Pero este efecto no es el único, en el modelo una bicicleta con ruedas de masa nula sigue siendo estable. Tampoco es cierto que las bicicletas con ruedas pequeñas sean inestables.
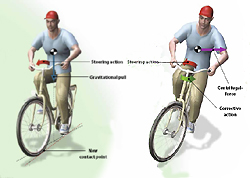
Ahora, gracias al modelo, se sabe que se da una combinación de fuerzas que garantiza la estabilidad de la bicicleta. Por ejemplo, la inclinación y el cambio de dirección explican por qué cuando deseamos cambiar de dirección a la derecha tenemos que torcer primero un poco a la izquierda. Esta acción produce una fuerza que hace que la bicicleta se incline al lado contrario hacia el cual deseamos ir. Además este mecanismo explica por qué nos caemos si montamos en bici muy cerca del bordillo, simplemente no podemos alejarnos de él sin golpearlo.
En cuanto al ángulo que forma la horquilla hacia adelante, llegan a la conclusión de que cuanto más grande sea éste más estable será la bicicleta cuando circule en línea recta, pero menos lo será al tratar de cambiar de dirección.
Otro factor importante es la distribución de masas. Si se mueve el centro de masa hacia adelante la bicicleta será más estable.
Como el modelo es capaz de predecir para un determinado diseño si la bicicleta será «nerviosa» o por el contrario estable, la industria ciclista está muy interesada. Así, Rob van Regenmortel, jefe de producción la compañía holandesa Batavus sigue de cerca el desarrollo de este trabajo de investigación.
Según este industrial para el diseño de sus bicicletas han jugado durante años con tres parámetros a la hora de diseñar una bicicleta: la geometría general, la distancia entre ejes y el ángulo que forma la horquilla. Las elecciones fueron hechas por los fabricantes en el pasado y rara vez se desvían del diseño básico porque simplemente parece funcionar bien. Según él, gracias a este nuevo modelo podrán diseñar pronto bicicletas con diseños orientados hacia grupos específicos de clientes.
Rob Van Regenmortel espera colaborar con Arend Schwab y Jodi Kooijman en el siguiente proyecto que estudiará el control humano de la bicicleta. La meta es estudiar la interacción entre bicicleta y ciclista para determinar las cualidades de maniobrabilidad del vehículo. De este modo se podría construir una bicicleta específica para cada ciclista.
Obviamente que sean unos holandeses los que estén detrás de este proyecto no es casualidad, cosa que puede comprobar cualquiera que haya ido a ese estupendo país donde todo el mundo monta en bici. Este vehículo es muy efectivo para distancias relativamente cortas, y ayuda a hacer el ejercicio tan necesario en la vida moderna.

Fuentes y referencias:
Nota de prensa de la Universidad Tecnológica de Delft.
Página de Cornell en la que se explica el modelo.
Artículo en Delft Outlook.
Artículo en pdf con gráficos.