El conjunto mandelbulb
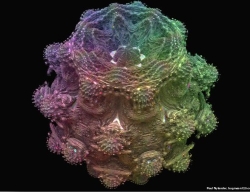
Proponen un nuevo conjunto fractal que en tres dimensiones tiene una características similares al conjunto de Mandelbrot (que se define en 2 dimensiones) y al que llaman conjunto mandelbulb.
|
|
|
Hay otros espacios a explorar que no son el espacio exterior. Son espacios abstractos habitados por objetos matemáticos. A veces su representación gráfica es increíblemente bella. Uno de los más famosos es el conjunto de Mabdelbrot que pertenece al plano complejo. Benoît Mandelbrot lo estudio en 1980 y por eso lleva su nombre, aunque en realidad éste fue descubierto por Pierre Fatou y Gaston Julia a principios del pasado siglo y representado por primera vez en 1978 Robert Brooks y Peter Matelski.
El conjunto de Mandelbrot, al estar contenido en el plano complejo, es plano. Sin embargo, posee una rica geometría. Es el arquetipo de fractal, de las figuras que son autosemejantes. Es decir, que cada parte, por pequeña que sea, tiene una forma similar a la de cualquier otra parte a cualquier escala.
Hay muchos ejemplos de fractales que se pueden construir de una manera sencilla. Uno de ellos puede ser el de la curva de Koch, que contiene un área finita bajo un perímetro infinito de dimensión fractal 1,26. Y es que otra característica de estos objetos es que tienen, en general, dimensión fraccionaria.
Además de estas características extrañas, el conjunto de Mandelbrot posee valor en Ciencias de la Computación. Se obtiene por recursión, iterando una función compleja (que usa números complejos) una y otra otra vez, concretamente esta fórmula:
zt+1 = zt2 + c
El algoritmo utilizado para representar el conjunto es como sigue:
Para cada punto c perteneciente al plano complejo.
– Fijar z0 =0
– Iterar desde t=1 hasta tmax
Calcular zt = z2t + c
Si |zt| > 2 salir del bucle
– Si t < tmax pintar c de blanco (el punto no pertenece al conjunto)
– Si t = tmax pintar c de negro (el punto pertenece al conjunto)
Como se puede apreciar, un punto pertenecerá o no al conjunto si el módulo del punto iterado tmax veces cumple o no una condición dada, si converge o no.
El conjunto, una vez llegamos a una profundidad de exploración dada por tmax, viene a ser algo así:

|
Los puntos coloreados (que no son negro) corresponden a números que no pertenecen al conjunto y para los que se ha asignado un color en función de lo supuestamente «lejos» que se han quedado de él. Si aumentamos mucho el número de iteraciones, y escogemos regiones cada vez más pequeñas, podemos apreciar la autosimilitud y la intrincada estructura de este objeto que algunos han llegado a calificar como monstruo. Es decir, aparecen nuevos detalles al aumentar la resolución, a todas las escalas estudiadas, e incluso aparecen “copias” del conjunto entero a resoluciones finísimas.
Lo más fascinante quizás sea que se puede demostrar que el conjunto de Mandelbrot es incomputable. Hay varios tipos de incomputabilidad, pero en este caso nos referimos a si podemos contestar la pregunta de si un programa se detendrá o no (un problema de decisión). Asumimos además que el programa que se quiere comprobar termina cuando alcanza una solución a un problema determinado y no lo hace si no la encuentra.

|
Alan Turing demostró que hay muchos problemas que no son computables y que, por tanto, algunas veces no podemos decir si un programa se detendrá o no. Una vez que un modelo de computación tiene la habilidad de estudiarse a sí mismo paga el precio de no ser capaz de parar bajo un conjunto apropiado de circunstancias (ciertas o erróneas).
Recordemos que Gödel demostró que todo formalismo matemático lo suficientemente complejo para que sea consistente es necesariamente incompleto. Pues bien, el teorema de Gödel es un caso particular del de Turing, ya que cualquier afirmación matemática puede ser implementada en un programa.
Por tanto la pregunta «¿Hay una demostración matemática para esta afirmación?» es equivalente a «¿Parará el programa?».
En realidad el algoritmo antes expuesto no representa el conjunto de Mandelbrot, sino una aproximación a él. Esto se debe a que hemos truncado el cálculo a una profundidad dada (tmax). Habrá puntos que hemos calificado como no pertenecientes al conjunto que si hubiéramos esperado más tiempo (más iteraciones) hubieran convergido y cumplido el criterio. Y da lo mismo si aumentamos el número de iteraciones, porque seguirá habiendo puntos para los cuales exista el mismo problema (y no sabremos a priori cuáles son). Esto quiere decir que para algunos puntos del plano complejo nunca sabremos si pertenecen o no a este conjunto tan singular.
Así que, como vemos, el conjunto de Mandelbrot da para mucho más que unas figuras atractivas. Pero como hay que captar la atención del lector de alguna manera podemos seguir con esta historia y publicar figuras realmente bonitas sobre este tema, concretamente sobre un nuevo conjunto, ente que además nos ha servido para contar todo lo anterior.
En los años ochenta hubo una auténtica fiebre por parte de los aficionados a la hora de calcular y representar el conjunto de Mandelbrot con mayor resolución, sobre todo a través del seguimiento que hizo Sicentific American (el que escribe todavía recuerda leer esos artículos sin entender mucho los detalles). Se inventaron atajos y algoritmos que permitían un cálculo que se hacía cada vez menos llevadero para lo ordenadores conforme se aumentaba la resolución.
Como todas las cosas, pasó de moda, pero desde entonces se esperaba descubrir conjuntos similares que tuvieran toda esta rica gama de características, a poder ser incluso en dimensiones superiores.
Lo más que se llegó a descubrir fue un conjunto similar en cuatro dimensiones del cual se representaban cortes tridimensionales que parecían bastante pobres.
Obviamente había fractales tridimensionales que se podían construir de manera sencilla, pero, o bien eran totalmente estocásticos, o bien completamente regulares. Ninguno captaba la filosofía del conjunto de Mandelbrot. Y los algoritmos de iteración que se proponía en 3D no mostraban un comportamiento fractal real. Los trucos de hacer girar sobre sí mismo al conjunto de Mandelbrot tampoco proporcionaban resultados satisfactorios.
Ahora se propone un conjunto contenido en el espacio tridimensional que, si bien no se ha demostrado que sea tan rico matemáticamente como el de Mandelbrot, sí produce imágenes comparables. Denominan al nuevo conjunto como «conjunto mandelbulb», se supone que por similitud fonética con el de Mandelbrot y porque se parece a un bulbo (bulb).
Daniel White, un británico aficionado al tema, posee una página web en donde muestra algunos ejemplos del conjunto mandelbulb calculados en los últimos dos años.
Para crear el nuevo conjunto White se vale de coordenadas esféricas y de una función iterada con una filosofía similar a la empleada en el caso del conjunto de Mandelbrot.
Las primeras versiones del algoritmo producían objetos que carecían del detalle fractal fino que tiene el conjunto de Mandelbrot, pero gracias al foro sobre fractales y a la cooperación con otros aficionados se ha llegado a una formula o fórmulas que producen objetos increíblemente bellos, aunque no sean equivalentes a un Mandelbrot tridimensional.
Todavía queda por introducir rigor matemático en este tema y está por ver si al final se consigue algo análogo al conjunto Mandelbrot en tres dimensiones, pero de momento nos podemos deleitar con unas bellas y góticas imágenes.
GALERÍA
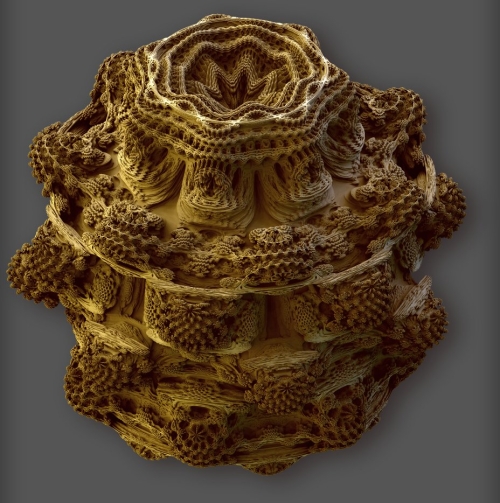
Esta figura representa el conjunto mandelbulb:
|
Aquí un detalle de ese conjunto calculado por David Makin:

|
White llama a esta región del conjunto la cueva de los secretos perdidos:

|
A los aficionados a la coliflor romanesca les encantará esta imagen:

|
Ampliaciones sucesivas de la región anterior nos proporcionan:

|

|
Estas otras regiones evocan a corales submarinos:

|

|
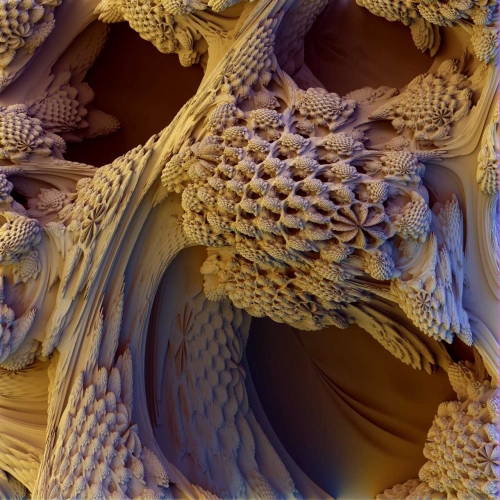
Según White esto recuerda a una colmena:
|
La espina de mandelbulb le será familiar a todo aficionado al conjunto de Mandelbrot:

|
Helado en Neptuno:

|
Para los amantes de los paisajes kársticos:

|
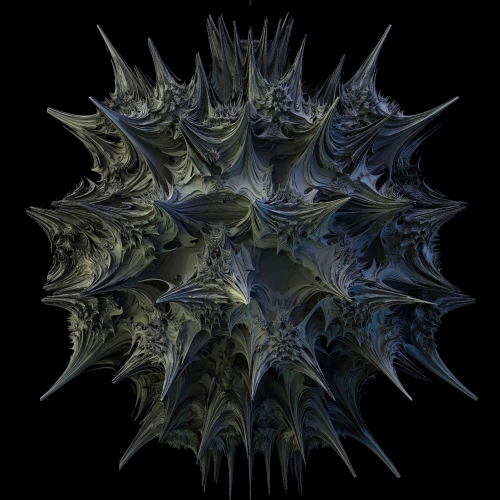
Las ecuaciones admiten variaciones que dan como resultado otros conjuntos igual de interesantes, como estos de aquí:
|

|
En la página web de White se pueden encontrar estas mismas imágenes en alta resolución y muchas otras, así como el algoritmo para obtenerlas.
Fuentes y referencias:
Página web de White.
Vídeo 1.
Vídeo 2.
Vídeo 3.
Vídeo 4.
Página de Wikipedia.
Ejemplo de imagen en alta resolución.
18 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





jueves 19 noviembre, 2009 @ 6:27 pm
Realmente apasionante. En esta ocasión se puede decir que el arte imita a la naturaleza… Me da la impresión de que sobre el tema de los fractales se habla mucho y hay mucha bibliografía, pero que sigue siendo un tema extraño y difícil de entender y que siempre está a punto de tener alguna aplicación «práctica» (¿qué significará esta palabra?) en cosas como la física. Se habla incluso de que el espacio tiempo podría tener una estructura «fractal». Recuerdo 2 libros : Caos, de James Gleick, y también La Nueva Mente del Emperador de Roger Penrose que pasaban sobre estos temas del caos, computabilidad, conjunto de Mandelbrot etc…, pero yo también he de admitir que son temas difíciles de entender… Para mí, lo mejor las imágenes.
Saludos fractales.
jueves 19 noviembre, 2009 @ 7:31 pm
En la teoría de símplices causales se predice que el espacio es fractal: http://neofronteras.com/?p=2614
En cuanto a la utilidad práctica de los fractales se utilizaron en su día para comprimir imágenes (ya en desuso), pero lo más tecnológico ha sido la creación de antenas fractales para telefonía móvil capaces de recibir y emitir en distintas gamas de frecuencias. La compañía Fractus las comercializa.
En cuanto a estas nuevas imágenes a algunos les produce cierto desasosiego. Son un poco oníricas en el sentido de pesadilla gótica.
Aunque es normal que los fractales imiten la naturaleza porque la Naturaleza tiene cierta fractalidad sea el brecol (o coliflor) romanesco, una descarga eléctrica, un helecho, el Gran Cañon, etc. La razón es que la génesis es la misma, son construidos por procesos iterativos, recursivos o estocásticos.
jueves 19 noviembre, 2009 @ 8:27 pm
Preciosas imágenes. La belleza de las matemáticas. Aunque eso del desasosiego «gótico» tiene algo de cierto, lo puedo constatar por mi mismo. Otro ejemplo de fractalidad lo es la hojita sagrada de los «rastafaris».
jueves 19 noviembre, 2009 @ 8:47 pm
Estimado Lluís
Casi todas las hojas tienen estructura fractal, incluida la del cáñamo.
Sobre Penrose tiene un comentario en el otro post.
viernes 20 noviembre, 2009 @ 11:14 am
Si ya nos quedamos impresionados con la representacion en 2D de los fractales, esto es realmente increible y bonito…
Son imagenes que nos demuestran que cada vez estamos mas cerca de cuantificar toda la superficie de «algo», en 3D…
Almenos en la coliflor lo vamos a tener facil…
;)
Un saludo.
viernes 20 noviembre, 2009 @ 11:19 am
Orgánico, con el vértigo que producen los infinitos… y la belleza de resumirse en una ecuación
viernes 20 noviembre, 2009 @ 1:40 pm
Impresionante. Recuerdo que a principos de los 90 (o últimos de los 80), tenía un programita que reproducía fractales en la pantalla de fósforo verde de mi ordenador. Con un disco duro de 10 megas (nada menos!). PCfract creo que se llamaba. Tardaba una media hora en dibujar una pantalla completa del Mandelbrot y yo no podia dejar de mirar, para desconcierto de mi pareja, que decía que estaba chiflado. Otro ejemplo de fractal natural particularmente bello: el crecimiento de la pirolusita entre láminas de mica.
Cordiales saludos.
viernes 20 noviembre, 2009 @ 4:41 pm
Apreciado RicardM:
Algunos cristales efectivamente crecen de manera fractal, incluidos los de hielo o los de pilorusita. Hay fractales que crecen por agregación como el que forma el hollín. El sistema venosos del corazón (o cualquier órgano altamente irrigado), los paisajes montañosos o los erosionados también lo son. La ruptura de un dieléctrico por una descarga, un CD «frito» en un microondas…
Por cierto, seguro que le gustará el vídeo número 2.
viernes 20 noviembre, 2009 @ 8:00 pm
A cuento del comentario de RicardM, y aunque sea offtopic, se puede decir que es casi generalizada la distinta actitud que tienen las mujeres y los hombres sobre este tipo de cosas. Al final hay una componente de juego, de curiosidad por las cosas, que las mujeres parecen no tener. Aunque ellas, en compensación, tengan actitudes más prácticas que los hombres.
En general no parecen entender por qué nos quedamos fascinados con la reconstrucción del conjunto de Mandelbrot, las maravillas de un puntero láser verde para señalar estrellas, un juego de ordenador o las cualidades del último chisme electrónico. A veces parece incluso molestarles ese supuesto comportamiento de «niño grande».
Quizás ese tipo de cosas las produce el mismo mecanismo que nos hizo fabricar herramientas, puntas de flecha o arcos de caza en el Paleolítico.
Sería interesante que alguien estudiara este tipo de cosas.
sábado 21 noviembre, 2009 @ 10:12 am
Queridos cocos (siempre incluido Neo en ese nombre -que me inventé- por ser el más prolífico):
No sabeis cómo agradezco tan bello artículo y tan enteradas opiniones. En su 2, Neo me envía a «Más allá de las cuerdas» -aunque no estemos en un combate de lucha- artículo que no conocía porque durante algunas temporadas me fue imposible dedicar ni un minuto a mi satisfacción preferida que es leeros. Y allí, un comentario me lleva a unos ensayos sobre el tiempo que fueron premiados. ¡Cuánto lamento haberme perdido en su día estas maravillas!
Muchos creen que matemáticas -e incluso ciencia- y belleza son incompatibles. Este artículo y alguna literatura demuestran que no. Muy al contrario, ilustran su intimidad.
Un gran amigo discutió conmigo sobre este tema y le dije que iba a hacerle un poema sobre algún número. Lo puso en duda y añadió que, en todo caso carecería de sentimiento. Hice unos veinte o treinta, muchos perdidos pues he cambiado de residencia tres veces en cinco años.
Me tomo la licencia de dedicaros los versos finales del primero de ellos aunque esto sea una página científica porque pretendo convencer de esa, mi certeza y porque no se me ocurre otra manera de pagar vuestra lejana y deseada compañía.
Debo aclarar que hay tres personajes centrales en todo el poemario resultante: un maestro al que recuerdo con gran cariño, un niño imaginario, como esos números, y yo en mi niñez:
El maestro, con amoroso acento:
«¿Sabrás decir, chiquillo, qué es el uno?»
Silencio largo, risas.
«Es un dedo»,
dice el niño de ilusión y esperanza.
Y el maestro lo busca y no lo encuentra.
¿Donde está ese niño divino?
¿donde está ese niño del aire?
¿donde está ese niño del agua?
Y yo me quedo absorto,
meditando,
pues ya sé qué es el uno
mi dedo levantado.
Uno es el árbol solo;
uno soy si estoy solo.
Allá adentro
muy dentro en mi conciencia
eso estaba muy claro:
soledad es el uno.
Un fuerte abrazo a todos y mil perdones por atreverme a tanto.
sábado 21 noviembre, 2009 @ 11:59 am
Estimado Tomás:
Es un lujo contar con lectores como usted.
sábado 21 noviembre, 2009 @ 6:54 pm
No sólo es un lujo para Neo, imagino que lo es para muchos de nosotros; los que pudiéramos llamar «comentaristas habituales», al menos.
lunes 23 noviembre, 2009 @ 7:52 am
La palabreja «cocos» designa, abreviando, precisamente a los comentaristas, pero creo que es mejos incluir a todos porque lo de habituales no tiene los límites definidos.
El lujo es para mí, al poder conversar con vosotros sobre estos temas, que Neo provee.
En resumen, que nos hemos metido en un lujerío que no hay quien lo aguante.
Un fuerte abrazo.
lunes 23 noviembre, 2009 @ 11:06 am
Base empírica; ya sé que las matemáticas deductivas no requieren verificación en su sistema interno de ecuaciones, pero, dada la similitud analógica de las representaciones visuales de mandelbrot, deberiamos estudiar formaciones geológicas, y formas rocosas de vida submarina, y ver si estas estructuras reales son mandelbrot, y en qué sentido y hasta que puntos.
Lo que me causa estupor es la inadecuación del lenguaje discursivo, la dialéctica retórica y sofistica, para comprender los laberintos matemáticos, que se refieren a espacios no verbalizables pero si matematizables.
¿No requeriríamos un metalenguaje propiamente dicho para aproximarnos holísticamente al todo contenido en la parte? Un lenguaje donde una cada palabra co-implique al resto, pero de modo muy preciso, asi como «dos» implica «uno más uno», un lenguaje asi…¡tendría la precisión de la aritmética!
lunes 23 noviembre, 2009 @ 11:32 am
Las matemáticas siempre necesitan de verificación. Los teoremas se demuestran, no se inventan.
Lo siento, pero lo que causa verdadero estupor es su lenguaje Juan Diaz, generalmente no se le entiende y lo poco que se le entiende deja claro que la ciencia no es lo suyo. Sólo le interesa una interpretación a su gusto de los resultados científicos aquí expuestos, tergiversándolos para así dar soporte a una visión que no es científica, por muy respetable que sea, y aunque no se sepa muy bien cuál es.
Por cierto, entre las peores palabras puestas de moda recientemente está «holística», sólo comparable a la infame «sinergia».
lunes 23 noviembre, 2009 @ 6:49 pm
Reconozco que en general el enfoque que tenemos las mujeres es distinto que el de los hombres, aunque habemos algunos «seres intermedios», por llamarnos de algún modo, que no actuamos del mismo modo que la mayoría.
Por ejemplo, a mí siempre me han parecido bellísimas las imágenes de los fractales, y me pasaba largo rato en el metro la raza (hay una sección dedicada a la ciencia con una representación del conjunto de Mandelbrot) tratando de ver más a detalle, lo cual desesperaba a mis amigas, aunque no a mi novio. Aunque lo que siempre me ha desesperado a mí es la dificultad que tengo en entender el planteamiento matemático, y mi poca habilidad para la programación. Pero la curiosidad ahí está.
¿Será esta una actitud muy poco femenina?
¿Será por eso que no tengo novio? Tal vez.
Que la pasen bien
lunes 23 noviembre, 2009 @ 11:55 pm
Estimada Gladia:
Ni generalizar es justo, ni aunque el tópico sea real siempre se está en la media estadística, suele haber fluctuaciones.
Pero como método para provocar comentarios femeninos el 9 ha surtido efecto. :-)
jueves 26 noviembre, 2009 @ 6:29 pm
Ja, ja, ja, eso es muy cierto. No cabe duda de que siempre hay algunos temas que nos hacen saltar. Punto para Neo.