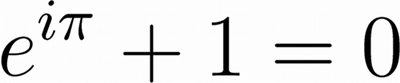NeoFronteras

Desarrollan un programa informático imbatible al póquer Texas Hold ‘Em a dos jugadores.

El primer juego de mesa en ser resuelto completamente (además de las tres en raya, claro) fue el de las damas. Y desde hace tiempo hay programas de ordenador que ganan a maestros del ajedrez, pero, hasta ahora, no había uno que fuera imbatible jugando al póquer. (leer más…)

Unos psicólogos tratan de estudiar la belleza de las ecuaciones matemáticas.

Siempre nos ha parecido difícil definir la belleza, pero desde la época de Platón dotamos a la misma de una cualidad especial, casi externa a la de los individuos que la experimentan. Pero ese placer que experimentamos al contemplar la belleza es puramente psicológico. (leer más…)

Un profesor universitario desafía la visión tradicional de las Matemáticas como una herramienta independientemente del ser humano que es muy efectiva a la hora de describir los objetos del mundo físico.

La sombra de Platón es alargada y aún hoy en día de deja sentir su influencia. Esto pasa sobre todo en las Matemáticas. ¿Tienen los objetos matemáticos una existencia aparte de la mente humana o son simplemente objetos culturales producidos por la mente humana? La primera posibilidad sería la platónica y es la que adoptan la mayoría de los matemáticos. Según esta visión cualquier otra civilización extraterrestre llegaría a los mismos resultados matemáticos que nosotros. Las Matemáticas estarían en “algún” lugar dispuestas a ser descubiertas.
Al otro extremo no platónico tenemos a los ingenieros que simplemente se valen de las Matemáticas para modelar sus proyectos. En el caso intermedio se sitúan los físicos, de los cuales los teóricos serían los más platónicos. Además parece que los físicos se confiesan más platónicos en público de lo que luego lo son en la intimidad. (leer más…)

Dos resultados sobre números primos nos acercan a la demostración de conjeturas famosas.

La función Π contabiliza los primos:.

Todos aprendimos de pequeños que los números primos son aquellos que sólo son divisibles por ellos mismos y por la unidad. Además, según el convenio acordado por los matemáticos, el 1 no es primo. Además sabemos desde la Grecia clásica que hay infinitos números primos.
Hay muchos aspectos interesantes en el tema de los números primos. Uno de ellos es que son los números fundamentales, pues cualquier otro número se puede generar a partir del producto de un conjunto de números primos. También es complicado generar números primos muy grandes, entre otras cosas porque, según avanzamos a lo largo de la secuencia de números enteros, los primos son cada vez más escasos y dispersos. (leer más…)

Descubren el primo de Mersenne más grande hasta la fecha y, por tanto, mayor primo conocido. Hace el número 48 de este tipo de números primos.

El proyecto Great Internet Mersenne Prime Search (GIMPS) ha anunciado el descubrimiento del primo de Mersenne número 48. El método empleado es el de la computación distribuida en la que muchos voluntarios permiten el uso de CPU de sus máquinas. No es la primera vez que se descubre un número primo de este tipo con este método por esta misma organización.
Los números de Mersenne son del tipo M_n = 2ⁿ – 1 siendo los primeros 1, 3, 7, 15, 31, 63, 127, … Los primos de Mersenne tienen un origen curioso y están relacionados con los llamados números perfectos. Euclides en el año 350 antes de nuestra era estudió este tipo de números. Toman el nombre de Marin Mersenne (1588-1648), monje y matemático originario de Francia, quien propuso una conjetura para los valores que tendría que tener el exponente “n” para que el resultado fuera primo. (leer más…)

Según un estudio es muy difícil que los participantes en los mercados financieros se comporten racionalmente aunque así lo quieran y, por tanto, la teoría de juegos no puede hacer buenas predicciones en ese caso.

Si usted nunca gana en juegos complejos que requieren cierta destreza como el póker o el ajedrez puede que haya una razón. Según Tobias Galla (University of Manchester) y Doyne Farmer (Oxford University, Santa Fe Institute) simplemente es imposible aprender completamente algunos juegos o son demasiado complejos para que la mente humana los comprenda completamente.
Estos investigadores corrieron miles de simulaciones en las que dos jugadores participaban en diversos juegos para ver cómo el comportamiento humano afecta el proceso de toma de decisiones. (leer más…)

Han publicado lo que parece ser una demostración revolucionaria de la conjetura ABC.

La aplicabilidad de la ciencia es muy variada. Así, si nos fijamos en la Biología comprobaremos que la mayoría de sus preceptos sólo son aplicables a la vida terrestre, aunque supongamos que otros pueden ser compartidos con otros tipos de vida hipotética en otros lugares del Universo. Digamos que la Biología no es universal. La Geología tiene mayor aplicabilidad fuera de la Tierra, pero a falta de información externa, sabemos más sobre nuestro planeta que sobre otros. Sin embargo, la Química o la Física son universales y sus leyes son aplicables a cualquier punto del Universo. (leer más…)