Química activa en exoplaneta revelada por el telescopio James Webb
El Telescopio Espacial James Webb ha producido la información espectral más detallada sobre un exoplaneta, convirtiéndolo en el mundo que mejor conocemos su atmósfera después de los principales planetas de nuestro Sistema Solar.

|
El Telescopio Espacial James Webb (JWST) acaba de marcar otra primicia: un retrato molecular y químico detallado de la atmósfera de un mundo distante.
El conjunto de instrumentos altamente sensibles del telescopio se enfocó en la atmósfera del exoplaneta WASP-39 b, que es un planeta tan masivo como Saturno que orbita muy cerca de una estrella que está a unos 700 años luz de distancia de nosotros y que gira a su alrededor en solo cuatro días terrestres.
No se cree que WASP-39 b sea habitable, pues tiene una temperatura estimada de 900 C y una atmósfera compuesta principalmente de hidrógeno. Pero el nuevo trabajo allana el camino para encontrar pruebas potenciales de vida en algún otro planeta habitable.
Aunque otros telescopios espaciales, incluidos Hubble y Spitzer, revelaron previamente en su día compuestos de la atmósfera de este planeta, los nuevos espectros proporcionan un conjunto completo de átomos, moléculas e incluso signos de química activa y nubes.
«La claridad de las señales de varias moléculas diferentes en los datos es notable. Habíamos predicho que íbamos a ver muchas de esas señales, pero aún así, cuando vi los datos por primera vez, me quedé asombrada», dice Mercedes López-Morales (Centro de Astrofísica, Harvard & Smithsonian).
Los datos más recientes también dan una pista de cómo se verían de cerca estas nubes en los exoplanetas, pues estaría fragmentadas en lugar de constituir un manto único y uniforme sobre el planeta.
|
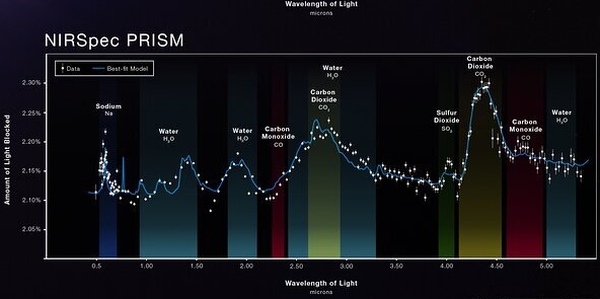
Los espectros de transmisión fueron obtenidos gracias a los tránsitos que este planeta efectúa sobre su estrella desde nuestro punto de vista, que hace que su atmósfera absorba selectivamente distintas longitudes de onda. Los investigadores proponen modelos de atmósferas y buscan el que mejor coincide con los datos. De este modo pueden predecir aspectos como su composición.
Los hallazgos son un buen augurio sobre la capacidad de JWST para realizar la amplia gama de investigaciones sobre exoplanetas que se espera. Eso incluye sondear las atmósferas de planetas rocosos más pequeños como los del sistema TRAPPIST-1, incluidos los que tengan temperatura propicia para la vida y que esto se revelara por espectroscopia de transmisión. En ese sistema, una pequeña estrella enana roja está orbitada por siete mundos del tamaño de la Tierra, algunos de los cuales podrían ser potencialmente habitables.
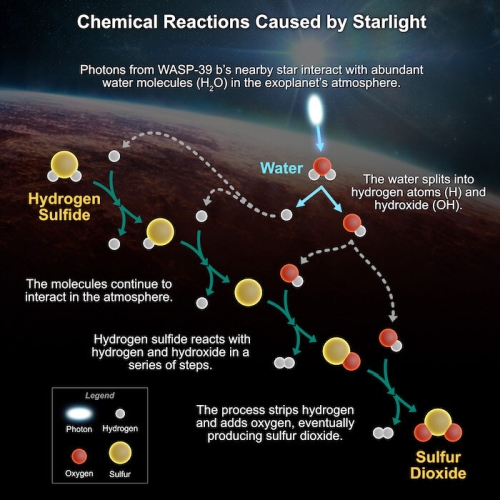
El conjunto de descubrimientos se detalla en un conjunto de cinco borradores de artículos científicos presentados recientemente y disponibles en el sitio web de preimpresión arXiv. Entre las revelaciones sin precedentes se encuentra la primera detección en la atmósfera de un exoplaneta de dióxido de azufre, una molécula producida a partir de reacciones químicas provocadas por la luz de alta energía de la estrella madre del planeta. En la Tierra, la capa protectora de ozono en la atmósfera superior se crea de manera similar.
|
«La sorprendente detección de dióxido de azufre finalmente confirma que la fotoquímica da forma al clima de los ‘saturnos calientes’. El clima de la Tierra también está determinado por la fotoquímica, por lo que nuestro planeta tiene más en común con los ‘Saturnos calientes’ de lo que sabíamos anteriormente», dice Diana Powell (NASA).
«La fotoquímica, debido a que es un proceso tan importante aquí en la Tierra, es probablemente un proceso importante en otros planetas potencialmente habitables. Solo hemos podido comprobar nuestra comprensión de la fotoquímica en nuestro Sistema Solar. Pero los planetas alrededor de otras estrellas nos dan acceso a condiciones físicas completamente diferentes», dice Jacob Bean, (Universidad de Chicago en Illinois).
La proximidad del planeta a su estrella anfitriona, ocho veces más cerca que Mercurio de nuestro sol, también lo convierte en un laboratorio para estudiar los efectos de la radiación de las estrellas anfitrionas en los exoplanetas. Un mejor conocimiento de la conexión estrella-planeta debería traer una comprensión más profunda de cómo estos procesos crean la diversidad de planetas observados en la galaxia.
Otros componentes atmosféricos detectados por JWST incluyen sodio, potasio y vapor de agua, lo que confirma observaciones previas de telescopios espaciales y terrestres, así como el encuentro de signos de agua adicionales, en longitudes de onda más largas, que no se habían visto antes.
Así, los datos de NIRISS muestran indicios de la presencia de potasio, agua y monóxido de carbono. NIRCam muestran señales notables de agua. Los datos de NIRSpec indican agua, dióxido de azufre, dióxido de carbono y monóxido de carbono. Finalmente, datos adicionales de NIRSpec revelan todas estas moléculas, así como el sodio. Las líneas de absorción obvias de metano y sulfuro de hidrógeno estaban ausentes de los datos. Si están presentes, estas moléculas se encuentran en niveles muy bajos.
Según Eva-Maria Ahrer (Universidad de Warwick), los resultados también mostraron una relación relativamente baja de carbono a oxígeno en el planeta. Esto sugiere que WASP-39b absorbió previamente una gran cantidad de agua en forma de hielo, probablemente cuando estaba en una posición diferente, y sugiere que se formó mucho más lejos en su sistema solar, quizás comparable a donde está Júpiter alrededor de nuestro Sol.
Se espera tal migración de Júpiter calientes, para explicar su proximidad a sus estrellas. Lo que no está claro es si se trata de un proceso lento que se da durante quizás decenas de millones de años, o un proceso más rápido. Conocer la composición de WASP-39b podría ayudar a los astrónomos a determinar qué ocurrió.
Al analizar con tanta precisión la atmósfera de un exoplaneta los instrumentos del JWST superaron con creces las expectativas de los científicos y prometen una nueva fase de exploración entre la amplia variedad de exoplanetas de la galaxia. El telescopio observará en diciembre un planeta llamado WASP-43b y se espera que esto revele detalles sin precedentes en el clima y la química del planeta.
JWST observará unos 70 exoplanetas en su primer año de trabajo que comenzó en julio pasado y que se extenderá hasta el próximo junio. WASP-39b proporciona un punto de referencia para esos estudios.
Copyleft: atribuir con enlace a https://neofronteras.com
Fuentes y referencias:
Preprint en ArXiv 1.
Preprint en ArXiv 2.
Preprint en ArXiv 3.
Preprint en ArXiv 4.
Preprint en ArXiv 5.
Ilustración de cabecera: Melissa Weiss/Center for Astrophysics | Harvard & Smithsonian.
Espectro: NASA, ESA, CSA, J. Olmsted (STScI) .
Esquema: NASA/JPL-Caltech/Robert Hurt; Center for Astrophysics-Harvard & Smithsonian/Melissa Weiss.
36 Comentarios
RSS feed for comments on this post.
Lo sentimos, esta noticia está ya cerrada a comentarios.





domingo 27 noviembre, 2022 @ 8:29 pm
Me pregunto. El día que encontremos un planeta con condiciones similares a la Tierra, pero que se halla a 1000 años-luz de distancia.
¿Cuá sería el próximo paso?
lunes 28 noviembre, 2022 @ 2:00 am
Estoy muy expectante con estos resultados: nos esperan 70 exoplanetas más para el próximo año, según nos informa Neo.
lunes 28 noviembre, 2022 @ 10:51 pm
¡Casi se me escapa el día de los Santos inocentes sin exponer mi «lo que sea» anual. Esta vez propongo que alguien sea capaz de demostrar o de razonar mi humilde conjetura que dice: «Cualquier número par puede ser obtenido por infinitas diferencias entre dos primos». Por ejemplo: 4 = 7-3 = 17-13 = 23-19 = … = 101-97 = … y así hasta infinitas diferencias de dos primos. En recuerdo de mi apellido -transformado- le he llamado Conjetura de Himen. Es que cada uno es como es y, por ello, mil perdones.
Abrazos.
martes 29 noviembre, 2022 @ 11:40 am
Amigo Tomás.
Vamos ver si te convence mi raciocinio para demostrar tu conjetura.
Voy a partir del Postulado (no se si correcto) de que la cantidad de Números Primos es infinita. Aunque intuyo que, a medida que avancemos mas y mas hacia el infinito, la densidad de estos se va haciendo cada vez menor, a costas de que la densidad de Números Compuestos va aumentando. Motivo: por ser el Conjunto de los números Naturales impares, igual a la suma de Primos más Compuestos.
Entonces, Al ser el conjunto de los Primos infinito, (P= p1, p2, p3, …pn….infinito) también lo será el conjunto ( C=combinaciones) de todas las parejas (diferencia) entre primos de este conjunto. P
O sea: Empezando por (p2-p,…pn-p1…), siguiendo por (p3-p1….pn-p1…)……(pn-p1)….(pn-p2)…(pn-p3)….infinitas diferencias.
Concluyo que, al ser este conjunto “C” de diferencias también infinito, forzosamente debe haber siempre por lo menos un elemento de este que, satisface tu conjetura.
Espero que se entienda mi raciocinio, y si incorrecto críticas.
Un fuerte abrazo.
martes 29 noviembre, 2022 @ 6:40 pm
Estáis demostrando una extensión de la conjetura de los primos gemelos, que supone que hay infinitos pares de primos cuya diferencia es 2. Yo leí esa demostración extendida, utilizando el mismo método, usando probabilidades, que es lo que, me parece, usa Eduardo en la suya, pero no tuvo demasiado éxito, o al menos se que nadie ha llamado al autor para felicitarle…. Si alguien está interesado en leerla, puede padírmela.
miércoles 30 noviembre, 2022 @ 8:02 pm
Creo que mi raciocinio anterior está equivocado. Motivo.
Como a medida que avanzamos en el conjunto de los Números Naturales Impares, la densidad de Primos se va haciendo menor. Intuyo que muy cerca del infinito su densidad tiende a llegar a cero, por tanto, en aquella región la densidad de Compuestos debe tender a uno.
Como la densidad de los números Naturales Pares es constante en todo su conjunto, (50 por ciento de los Naturales). Intuyo que, en aquella región, todos los números pares tienden a ser cubiertos por la diferencia de dos Compuestos, lo que excluye que sean cubiertos por la diferencia de dos Primos.
Entonces no sobra ningún Número Par libre (a partir de aquella región) para ser cubierto por la diferencia de dos Primos.
O sea, en el infinito de los Números Naturales creo que tu conjetura falla.
Lo difícil es llegar hasta ese infinito para comprobarlo.
miércoles 30 noviembre, 2022 @ 11:02 pm
Muchas gracias, «petrus». Sí, te agradecería que lo enviases.
miércoles 30 noviembre, 2022 @ 11:03 pm
Muy agradecido, querido Eduardo. Primero: es un hecho la infinitud de los números primos y su demostración es bastante sencilla (Euclides, pero hay más), pero no la pongo par no extenderme. Segundo, es cierto que conforme los números se hacen mayores, el número de primos decrece en un mismo intervalo: p. ej., entre 1 y 100 hay 25; entre 900 y 1000, 14; entre 9900 y 10.000, 9 y entre 99.900 y 100.000 hay 6. Y no sigo para no cansar, pero parece evidente, aunque sé que existe un diagrama que lo corrobora, pero no recuerdo el nombre de su autor. El conjunto de los números pares es infinito; también el de números impares y, ciertamente, si el conjunto de números primos es infinito, también lo será el conjunto de las diferencias entre dos cualesquiera de ellos. Es decir, por si no queda claro (P = primo): Pares, infinitos; diferencias P1 – P2 infinitas parejas. Eso implica que podemos elegir el número par que se nos antoje, aunque me pregunto: ¿implica eso que siempre hallaré una diferencia par para ellos -o infinitas, como creo?
miércoles 30 noviembre, 2022 @ 11:16 pm
Perdón por la mala redacción de mi última frase. Quiero decir: ¿implica eso que siempre hallaré una diferencia entre un par de primos -o infinitas, como creo- igual a ese número par previamente escogido?
miércoles 30 noviembre, 2022 @ 11:28 pm
Me opongo a tu 5, querido Eduardo. Las premisas son casi aceptables, pero es nunca estaremos cerca del infinito. Podremos decir matemáticamente que cuando el límite de los números naturales impares tiende a infinito, la densidad de los números primos tiende a cero.
Ciertamente, al ser la densidad de los pares constante, cualquier par será obtenido por un montón de diferencias de pares (seguro que infinitos), pero eso no excluye que pueda serlo por pares de primos. Y es que, mi querido amigo, el infinito es larguíí-íí…simo
jueves 1 diciembre, 2022 @ 11:22 am
Amigo Tomás, Es que este concepto de infinito a mi se me atraganta. Mis neuronas no dan para tanto.
Creo que fue Cantor quien dijo algo sobre diferentes clases de infinitos.
No consigo entender ¿cómo puede ser infinito el conjunto de los Números Primos (dentro del conjunto de los Números Naturales Impares). Al ser su densidad tendiendo a cero.? Intuyo que en ese momento se agotan los Primos.
Intuyo que el conjunto de los Primos es diferente del conjunto de los Naturales Pares. Por ser la densidad de estos Números Pares homogénea, y la densidad de los Primos con gradiente decreciente tendiendo a cero.
Por tanto, en este mismo conjunto de Impares, la densidad de Números Compuestos tiende a cien por ciento.
Entonces al entrar en esta región la posibilidad de surgir algún Primo tiende a cero. lo que trae como consecuencia que no exista dos Primos, para que su diferencia cumpla tu conjetura.
Abrazos casi infinitos
jueves 1 diciembre, 2022 @ 12:49 pm
Además probado está de mil maneras. Yo te voy a dar una que me saco de la manga, sencillísima, y que no es más que una ligera variante de la de Euclides: Multiplicamos todos los números primos excepto el 2; pues si admito el 2 el producto será par y no me saldrá la demostración. Es decir:3.5.7.11.13.17.19.23., me quedo aquí pero hemos de seguir hasta ese infinito de Eduardo. Ese producto vale, salvo error, 3234846615. A este le sumamos 2 para que el resultado sea impar y sale 3234846617 (con este método, siempre acabarán en 7, pero eso no le quita validez) que, necesariamente, ha de ser primo. El anterior no puede serlo por ser par. Así que dividiendo por el producto de todos los anteriores, habrá de dar 2 de resto. Tampoco puede ser dividido por ninguno de ese producto, por lo que ha de ser, necesariamente primo. Salvo errores, dividido por 3, da resto de 2; dividido por 5,resto 2, etc. Siempre resto 2, y si lo dividimos por cualquier producto de esa secuencia de primos, también dará 2 de resto. Por tanto el número 3234846617 es primo. Es mi demostración; no tan elegante -evidentemente- como la de Euclides, pero válida. Y de ello se deduce que cualquier número, por grande que sea, dividido por el producto de todos los primos (excepto el 2) que le preceden, más 2, siempre dará un número primo, así que el conjunto de primos es infinito. Demostrado.
jueves 1 diciembre, 2022 @ 1:29 pm
Pero hombre, querido Eduardo, si tienes tantísimas neuronas y debes multiplicarla por no menos de 10 o 100 -no sé- para saber las conexiones, seguro que entiendes lo siguiente. Yo no recuerdo bien a Cantor, pero sí que si se puede establecer una relación uno a uno con los números naturales, entonces, esos dos infinitos son iguales. Veamos: el primero natural y el segundo, primo: 1=>2; 2=>3; 3=>5; 4=>7; 5=>11; 6=>13;… etc. (y perdón por los suspensivos con el etc., pero es que el infinito se lo merece todo). Esos dos infinitos son iguales o mejor, es tan infinito el uno como el otro. No sucede lo mismo con los irracionales, porque entre el 2 y el 3, por ejemplo, hay un número infinito de irracionales y no hay forma de construir una correspondencia. Entonces el infinito de los irracionales es mayor que el infinito de los naturales.
Y recordando a «petrus», también es tan infinito el número de parejas de primos gemelos como el de primos y el de naturales. Por ejemplo, sea el primer término natural y el segundo la pareja de gemelos: 1=>3# 5; 2=>5#7; 3=>11#13; 4=>17#19; 5=>29#31; 6=>41#43 y otra vez… etc. Así que, efectivamente, hay categorías de infinitos.
jueves 1 diciembre, 2022 @ 1:35 pm
Es que personalmente veo el 2=Primo, como que fuera de contexto, por pertenecer al conjunto de los pares. Pero bueno, tengo que aceptarlo, si se adopta como postulado.
No obstante creo que, aunque el conjunto de los Primos sea infinito, me parece que cuando este realmente llegue a infinito la densidad de Primos debe ser nula=0,
Lego a un impase, pues al mismo tiempo que el Conjunto de Primos es infinito, al llegar a este, se transforma en finito por llegar a densidad cero. Y por aquí soy forzado a parar. Mis neuronas no dan para más.
jueves 1 diciembre, 2022 @ 1:47 pm
No admito que tus neuronas no den para más, salvo que recordemos a K.afk.a y su obra «Metamorfosis» e, imitando a su sujeto, te conviertas en un gordísimo insecto.
Un abrazo infinito.
jueves 1 diciembre, 2022 @ 3:06 pm
Hola Tomas. La deducción que obtienes estableciendo una correspondencia entre los Naturales y los Primos en principio parece correcta.
Lo que no me encaja, es el concepto de que en el infinito de los infinitos (infinito elevado a la enésima) la densidad de Primos es nula. Por tanto, falla su correspondencia con los naturales.
Ahí es donde me atasco.
jueves 1 diciembre, 2022 @ 8:13 pm
La demostración a la que hago referencia está publicada en en ese foro del que alguna vez he escritp, diosoazar.com, en el tema Primos, que se puede buscar en la página principal arriba derecha etiqueta Buscar «primos». Se hace largo… y hasta usa un teorema de Dirichlet, pero creo recordar que acaba usando probabilidades… Los infinitos suelen ser intratables.
jueves 1 diciembre, 2022 @ 8:50 pm
Estimado tomás. sobre el #11. Cuando afirmas que «necesariamente debe ser primo», ¿ es seguro?. Puede ser primo o compuesto. ¿ por qué no puede ser compuesto ?. No lo veo claro. Euclides usa el mismo método casi, pero sabe que entre el número que se prueba y el producto de los primos menores que él puede haber primos mayores que el mayor que usas en el producto… Ejemplo: toma hasta el primo 17, tienes P=255255, le sumas dos, tenemos N=255257 que No es primo, pues tiene el factor 47 5431×47=255257. ¿Qué hago mal? creo que probarlo solo con los primos menores que él es olvidarse de muchos más números menores que él también, pero que no están en la lista de esos primos, como pasa con el 47 del ejemplo. Y sí, el 5431 sí que es primo.
jueves 1 diciembre, 2022 @ 9:51 pm
Buen artículo. No es habitable para humanos terrícolas, pero sí para muchos microorganismos extremófilos de la Tierra.
viernes 2 diciembre, 2022 @ 11:14 am
Querido amigo «petrus»: Pues tienes toda la razón. Está clarísimo. Bueno, por algo Euclides fue Euclides y yo soy un humilde yo. El efecto, el resultado puede ser primo o compuesto. Está claro que será primo respecto a sus componentes tras sumarles 2; será compuesto formado por sus primos previos. En mi razonamiento debería haber previsto lo que el gran maestro y decir: puede ser primo o compuesto, etc. y seguir el mismo razonamiento que él. Una vez aclarado, el fin es bueno: los primos son infinitos.
Desatascamiento de Eduardo: No, querido amigo, no falla su correspondencia con los naturales porque su densidad no es absolutamente nula: no acaban nunca, como lo demuestra el que haya infinitos primos, como hay infinitos naturales.
Bueno, más vale acabar con mi presunta «inocentada», porque veo que el compañero Alejandro se impacienta. Pero antes de tratar con él os quiero contar la que hice en un centro de esos que se dedican a fisioterapia, osteopatía y cosas así. Cada año hago alguna. Esta vez fue: Entro renqueando y quejándome de mis pies. Pregunto si hay algún médico pedrerastra. La dependienta se horroriza un poco. Entonces rectifico y digo: bueno, quiero decir si tienen algún piediatra. Me dicen que no e insisto: ¿y un pedólogo?. Me echaron.
Pues sin más que decir del 28-11-22 me despedo del tema y me voy con Alejandro.
viernes 2 diciembre, 2022 @ 11:32 am
Amigo Alejandro: Soy de tu misma opinión. Creo, y lo he dicho alguna vez, que en Marte hubo de haber vida y aún tengo la esperanza de que, en algún lugar protegido de los UV -por ejemplo en el subsuelo o/y en los polos-, haya alguna vida sencilla. Si, como sospechamos, la vida o sus principales componentes «vivos o casi vivos», vinieron cabalgando en esos pedruscos que llegaron a la Tierra, la Luna, Marte, etc., pues la posibilidad es clara. Así que veremos, que dijo el ciego.
Un abrazo.
viernes 2 diciembre, 2022 @ 11:45 am
Perdón, Alejandro: Creo, como tú, que algunos extremófilos terrestres podrían subsistir en Marte. La cuestión es si será moral y prudente llevarlos. Yo pienso que sí, pues nos otorgarían conocimiento, aunque habrá que meditarlo. De todas formas si va un/a humana/o, ya llevaremos, queramos o no, algún bicho. Y a nosotras/os -siempre las damas primero- ya somos una especie de extremófilas/os artificiales, o sea, fruto de la tecnología.
Chao.
viernes 2 diciembre, 2022 @ 6:37 pm
A fuerza de creernos superiores, por diferentes, a los demás seres vivos, hemos dividido la naturaleza en dos mitades, nosotros, y lo artificial por un lado y todo lo demás, vivo o muerto, todo lo no tocado por la varita mágica de la tecnología, al otro. Ahora bien, visto el problema desde fuera, un observador extracósmico nos vería tan naturales como el resto, y a la tecnología como un apéndice más de la naturaleza, aunque sea un apéndice que brote de lo que podría ser su parte más noble y evolucionada, su cabeza. El pájaro lleva las semillas del arbusto en el que se posó hasta lugares lejanos y el homo sapiens difunde sus virus y sus desechos ( como lo hace el pájaro) a lugares a donde el pájaro llegará cuando el homo lo lleve también. Admito que, hoy en día, considerar a todo como natural no es políticamente correcto y debería invitar, más bien, a respetar lo que llaman el medio ambiente, pero ello significa considerarme fuera de y enemigo de, el medio ambiente. Y creo que soy y somos medio ambiente. Lo que no debe ser óbice, cortapisa o valladar, creo que lo saco de La Codorniz, para evitar conductas que menoscaben, dañen o destruyan medioambientes sin una razón de suficiente peso, como sería la supervivencia de la especie humana…
viernes 2 diciembre, 2022 @ 8:31 pm
Es que los homos/as, somos así. Todo lo clasificamos, dividimos, subdividimos, etc. Por ejemplo seres vivos: animales, vegetales, hongos, protoctistas y moneras -prefiero las morenas, pero no forman reino, aunque lo merezcan tanto como las rubias, pelirrojas, calvas, etc.- Y, como bien sabes, dentro de cada reino, las subdivisiones que yo me aprendí así: «El rey domina con filo en clase el orden, familia, género y especie.» aunque hay más, como superfilo, subfilo, subespecie, etc. Y como bien dices, el «reino» mineral o -pedruscos- al que hay que sumarle gases y agua, por ejemplo, de los cuales todas/os hemos salido. (Ya ves cómo me enrollo solo para darte la razón). Y sí, seguramente no somos tan importantes. Cuando finiquitemos, otros bichos pervivirán, y cuando estos caigan, otros continuarán, hasta la fase final, cuando el Sol, harto ya, decida sumarse, a lo grande, al calentamiento global. Y Fin de fines.
viernes 2 diciembre, 2022 @ 9:14 pm
Alejandro, creo que te gustaría volver al artículo. Por ello te comento que ese WASP-39-b es un tiovivo bestial, ya que lleva una velocidad de -nada menos- que 132 km/s. Yo no me monto, porque, aunque mi cabeza sea una bola de billar, seguro que me despeino.
Saludos.
martes 6 diciembre, 2022 @ 1:50 pm
Mi hija Lucía quiere teclear un comentario:
Hola soy Lucia tengo 10 años me interesante que todos los cientificos y cientificas esteis descubriendo nuevos planetas y galaxias me gustaria a mi investigar sobre si hay extraterestres en algun planeta. Estos ultimos dias ha habido auroras boreales rosas. Hasta luego.
martes 6 diciembre, 2022 @ 6:35 pm
Estimada Lucía:
No sabemos aún si hay seres similares a nosotros o si hay vida en otros planetas. Puede que sea una búsqueda larga y difícil, por eso es importante que a las nuevas generaciones les interese este tema y se siga investigando en el futuro. Puede que seas tú la que en el futuro investigue estas cosas o que incluso lo descubra, así que tendrás que estudiar mucho en el cole. Y si al final te interesa otra carrera, no te olvides de apoyar la ciencia. Lo vamos/vais a necesitar.
Si quieres ver auroras y saber cómo se producen puedes ver este documental:
https://www.rtve.es/play/videos/somos-documentales/el-cielo-en-llamas/6303161/
miércoles 7 diciembre, 2022 @ 8:33 pm
¡Qué alegría me he llevado esta mañana al leer tu comentario, queridísima Lucía! Yo sé que tus papá y mamá, te están educando maravillosamente y que, cuando seas mayor, alcanzarás gran sabiduría.
-He comenzado esta mañana, pero he tenido que dejarlo y vuelvo ahora, sobre las siete de la tarde-.
Vamos a puntualizar: Si hay vida en algún planeta que no sea el nuestro, ya hay extraterrestres, aunque solo sean microbianos. Pero como yo sé lo muy curiosa que eres -seguro que te refieres más a algún ser inteligente-.
Si en la Tierra no hubiese caído el meteorito de Chicxulub hace unos 66 millones de años y que se cargó a los dinosaurios, pterosaurios (que volaban), ictiosaurios (que nadaban) -seguramente puedo poner etc.- de los cuales (descendientes de un tipo de dinos que tu papá te explicará mejor que yo) nos quedan las aves. Sí, el diminuto colibrí y la gran avestruz son descendientes de esos dinos. Pero un tal Russell imaginó que si no hubiese caído aquel tremendo pedrusco, algunos dinos hubiesen desarrollado una especie de humanoide al que llamó «dinosauroide», que no sería mamífero, sino saurio. Puedes verlo en las páginas que voy a intentar mandarte: https://maikelnai.naukas.com/2009/02/15/dinosaurios-inteligentes-la-hipotesis-del-dinosauroide/ y también en https://es.wikipedia.org/wiki/Dinosauroide
Espero que te interese y que te lo expliquen tu mamá y/o papá, porque si eso no hubiese sucedido, sería difícil que los homos estuviésemos aquí, y realmente, es posible que alguna especie de dino hubiese alcanzado una importante inteligencia y ¿sabes por qué? Pues porque se daban ciertas condiciones, como por ejemplo ser seres sociales y más, pero no quiero seguir para no aburrirte.
Dentro de unos años tú verás cosas que ahora, ni soñamos; sí, también en astronomía.
Un fuerte abrazo para ti y tus papás.
miércoles 7 diciembre, 2022 @ 8:40 pm
Veo que si pincho en las direcciones que te he mandado no te da acceso. Eso es porque el sistema me obliga a poner un punto detrás de cada «k». Los quitas y verás las páginas. Es muy curioso porque lo asemeja a un humano solo que con tres dedos, aunque lleva bañador, lanza y una bolsa para -imagino- guardar lo que cace.
jueves 8 diciembre, 2022 @ 1:40 am
Arreglado lo de los puntos tras la k.
jueves 8 diciembre, 2022 @ 10:39 am
Muchas gracias, admirado Neo. Es que, para esa tontería de las «k», no veo explicación. Es una letra de nuestro idioma poco frecuente, pero también lo es la «w». Imagino que son cosas del sistema. Lo que me alegra es que puedas salvar el problema.
Mil gracias.
jueves 8 diciembre, 2022 @ 10:39 am
Muchas gracias, admirado Neo. Es que, para esa tontería de las «k.», no veo explicación. Es una letra de nuestro idioma poco frecuente, pero también lo es la «w». Imagino que son cosas del sistema. Lo que me alegra es que puedas salvar el problema.
Mil gracias.
jueves 8 diciembre, 2022 @ 5:08 pm
Apreciado Tomás:
Eso se debe a la presencia de un plugin que fue creado para la comunidad de bloguers hace más de 17 años. En buena época sin redes sociales había mucha gente comentando en blogs y la habilidad de algunos de ellos para escribir correctamente era deficitaria. El plugin impedía escribir ciertas incorrecciones, entre ellas determinadas combinaciones de k y sus vocales. Se puede escribir kilo o kimono sin problemas. En castellano/español hay muy pocas palabras que contengan esta letra y muchas veces se pone por tontería. A veces incluso se escribe o escribía k en lugar de «que».
El problema es que ya no sé como se puede quitar, pues había que escribir parte del código en en la página principal.
No es más que un script que puede ser saltado si se desea.
viernes 9 diciembre, 2022 @ 12:08 pm
En efecto, casi toda mi descendencia pone «k» en vez de «que». Si quieren abreviar, es más lógico poner «q». Invadidos estamos de memes y memos. Yo mantengo mi posición en esta guerra como buen antediluviano.
Gracias por tus explicaciones.
lunes 19 diciembre, 2022 @ 1:40 am
¡¡Muy bonitas vuestras respuestas, queridos Neo y Tomás!!: no se anima a responder -tiene la disculpa de haber estado estos días con fiebre-, pero ha visto la mitad del vídeo de Neo y me ha dicho que le diga a Tomás qué le ha parecido el pollo del huevo de dinosaurio que se acaba de encontrar.
Muchas gracias, amigos.
lunes 19 diciembre, 2022 @ 8:09 pm
Si a ese «qué» que va detrás de Tomás, le quitas el acento, la frase puede tomarse como si Lucía hubiese adivinado que mi cabeza esta tan pelada como un huevo y que ella lo ha encontrado (por adivinado -un poco elíptico, ¿no?-)
Felices Navidades, queridísima familia.